1. 서 론
2. 재료 및 실험방법
2.1 측정 지점
2.2 입력자료
2.3 LightGBM 모형
2.4 모형구축
2.5 SMOTE를 이용한 입력자료 구성
2.6 모형 성능 평가 방법
3. 결과 및 고찰
3.1 LGBM 모형 결과
3.2 SMOTE 적용 비율에 따른 모형 성능 비교
4. 결 론
1. 서 론
강우 시 유량의 증가는 하천에서 많은 퇴적물을 이동시키며 탁도가 높아지는 원인으로 고 탁도는 주변 관계 지역의 안정적 물 공급과 하천 수 생태 환경에 다양한 부정적 영향을 줄 수 있다 (Schleiger 2000, Nasrabadi et al. 2016). 또한 고 탁도 원수 유입에 따른 정수장 응집제 주입량 및 역 세척 증가로 정수처리 비용이 높아지는 다양한 문제를 발생시킬 수 있어 지속적인 관리가 필요하다 (Kwon et al. 2004, Chung and Oh 2006). 하천의 탁도 예측을 통해 탁수로 인해 발생하는 문제를 대비할 수 있으며 이를 위한 기계학습 모형의 적용이 점차 늘어나고 있다 (Zounemat‐Kermani et al. 2021, Han et al. 2023).
Lu and Ma (2020)은 앙상블 머신러닝 모형인 RF (Random Forest)와 XGBoost (Extreme Gradient Boosting)에 데이터 노이즈 제거 후 단기 수질 예측을 수행하여 기존에 모형에 비해 높은 성능을 얻을 수 있는 것을 확인하였고 Gu et al. (2020)은 앙상블 기반의 RF와 Google에서 제공하는 위성 영상을 통해 원격으로 초 분광 감지 자료를 수집할 수 있는 Google Earth Engine을 결합한 새로운 하천 탁도 측정 모형을 제안했다. Kumar et al. (2022)는 홍콩 해양 탁도 예측을 위하여 인공신경망 (Artificial Neural Network, ANN)과 Support Vector Machine, 순환신경망 (Recurrent Neural Network)계열의 Long Short-Term Memory를 이용하여 정확도를 비교하였고 Iglesias et al. (2014)는 ANN을 이용하여 스페인 북부 하천 유역의 탁도를 예측하였다.
앙상블 모형은 분류와 회귀 방식 모두 적용이 가능하고 모형의 최적화와 같은 모형의 유연성을 확보할 수 있어 많이 사용되고 있는 기계학습 방법으로 환경 등 다양한 분야에 적용하기 위한 개발이 활발히 이루어지고 있다 (Asadollah et al. 2021). 앙상블 모형은 여러 개의 단일 모형을 통해서 도출한 결과를 결합하여 결정을 내리는 방법을 통해 단일 모형에 비해 과적합의 발생 가능성을 줄이고 상대적으로 우수한 성능을 얻을 수 있는 장점을 가지고 있다 (Dietterich 2000, Sagi and Rokach 2018, Zhang et al. 2018).
하천의 탁도는 강수량이 많은 특정 시기에 높은 수치들 분포하고 있으며 그 이외 시기에는 일정한 수치를 유지하여 자료 획득 시 데이터의 균형이 맞지 않는 불균형 현상이 일어나게 된다 (Alexandrov et al. 2007). 데이터 불균형 현상은 부족한 데이터 수로 인하여 기계학습 과정에서 특징을 구별하여 학습하는 것을 어렵게 하고 예측성능이 떨어지는 문제를 발생시킨다. 이를 해소하기 위해서 적절한 데이터를 확보하는 것이 좋은 방법이지만, 불가능한 경우가 많아 over-sampling과 under-sampling과 같은 데이터 불균형 해소 방법을 통해 데이터 불균형 현상을 극복하는 경우가 많다 (Uyun and Sulistyowati 2020, Xu et al. 2020, Shin et al. 2021, Kim and Park 2023).
본 연구에서는 앙상블 모형인 GBDT (gradient boosting decision tree)기반의 알고리즘 중 빠른 학습 속도와 우수한 성능을 가진 LightGBM (light gradient boosting machine)을 이용하여 금강의 주요 지류 중 하나인 미호강의 탁도에 따라 4개의 class로 구분하고 예측하는 모형을 구축하였고, 대표적인over-sampling 기법의 하나인 SMOTE (synthetic minority over-sampling technique)를 이용하여 데이터 불균형 해소 비율을 다르게 한 다양한 입력자료를 구축하고 이러한 입력자료의 불균형 해소 비율의 차이가 모형의 성능에 미치는 영향을 비교하였다.
2. 재료 및 실험방법
2.1 측정 지점
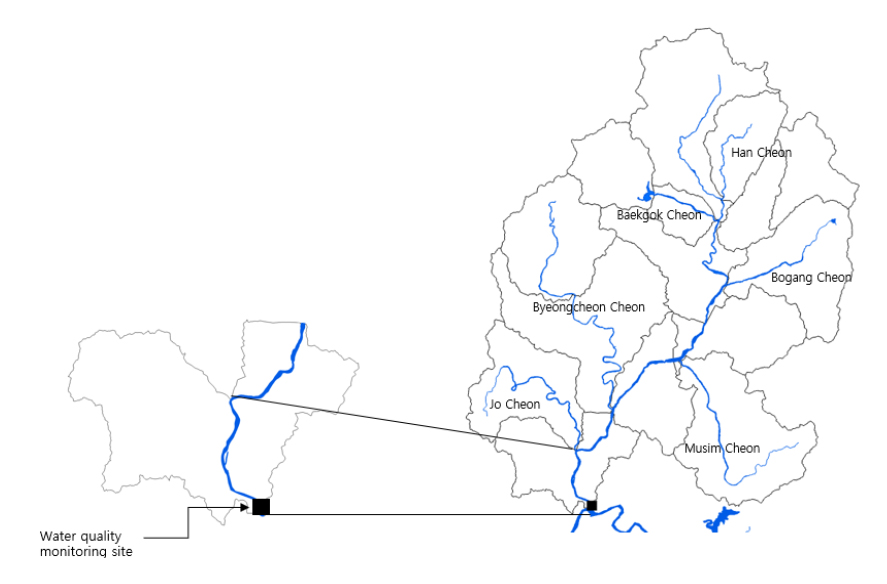
미호강은 충청북도 음성에서 발원하여 충청북도 청주시, 세종특별자치시를 거쳐 금강에 합류하는 금강 제1 지류 하천으로 1,855 km2의 유역 면적과 79.2 km의 길이를 가진 금강수계의 지류·지천 중 유역 면적이 가장 크고 도심 생활하수 및 축산 폐수 등의 다양한 오염물질이 유입되어 지속적인 수질관리와 어류, 저서성대형무척추동물 등 수중생물 서식환경 보호를 위한 수 생태 관리가 필요한 하천이다 (Fig. 1) (Kim et al. 2014, ME 2022).
2.2 입력자료
본 연구에서는 환경부 국립환경과학원에서 제공하는 물환경정보시스템의 수질 자동측정망 중 미호강 지점 (S03006)과 국가 수자원 관리 종합정보시스템에서 제공하는 실시간 유량 자료 중 세종특별자치시의 월산교 지점 (3011695)에서 2016년 1월 1일부터 2023년 12월 31일까지 측정된 일별 수질 자료 및 유량 자료를 활용하였다 (NIER 2023, WAMIS 2023). 측정자료 중 수온 (temperature, TEMP), pH, 전기전도도 (electrical conductivity, EC), 용존산소량 (dissolved oxygen, DO), 유량 (discharge, Q) 총 5개 항목을 모형의 구축을 위한 독립변수로 사용하였으며 탁도 (turbidity, T)는 예측의 대상이 되는 종속변수로 사용하였다. 본 연구에서는 탁도를 예측하는 분류 모형을 구축하였으며, 기존의 연구사례 등을 고려하여 탁도에 따라 10 NTU 미만은 class 1, 10 NTU 이상 30 NTU 미만은 class 2, 30 NTU 이상 100 NTU 미만은 class 3, 100 NTU 이상은 class 4로 분류하여 모형의 종속변수로 사용하였다 (Lin et al. 2004, Seo et al. 2011).
2.3 LightGBM 모형
LightGBM은 Microsoft에서 개발한 GBDT기반의 기계학습 알고리즘으로 GOSS (gradient-based one-side sampling)와 EFB (exclusive feature bunding)를 통해서 메모리 사용량을 감소시켜 학습 속도가 빠르면서 모형의 성능이 우수하다는 장점을 가지고 있다 (Ke et al. 2017). GOSS는 학습 과정에서 학습 자료의 기울기 (gradient)가 클수록 모형의 정보획득양 (information gain)에 주는 영향이 크기에 gradient가 큰 자료는 유지하고 gradient가 작은 자료들은 일부 배제하여 학습 자료의 수를 줄이는 방법이고 EFB는 입력 변수의 수를 줄이는 방법으로 입력 변수의 값이 0이 아닌 값을 동시에 가지지 않는 상호 배타적인 입력 변수들을 단일변수로 묶어 계산의 효율성을 높이는 방법이다 (Ke et al. 2017).
2.4 모형구축
측정 항목은 각각 TEMP 22.5%, pH 22.5%, EC 22.5%, DO 23.7%, T 31.3%, Q 0.27%의 결측 값을 포함하고 있으나 대부분의 결측 값이 T가 높지 않은 기간에 포함되어 있기에 결측 값 주변의 k개의 측정 자료로 결측된 지점의 값을 보간하는 KNN (K-Nearest Neighbor)을 이용하여 결측 값을 보간하였다. KNN은 python open source library인 scikit-learn을 이용하여 구현하였다 (Pedregosa et al. 2011).
모형 구축을 위해서 LightGBM open source library를 이용하였으며 (LGBM), 전체 자료 중 2016년 1월 1일부터 2020년 12월 31일까지의 자료를 학습 (training) 자료로 사용하고 2021년 1월 1일부터 2022년 12월 31일까지의 자료를 모형 성능의 검증 (testing) 자료로 사용하여 모형의 training 및 testing에 사용된 자료의 비율은 각각 71.45%, 28.55%로 구성하였다. 모형의 최적화 작업은 python open source library인 scikit-learn의 grid search를 이용하여 구현하였다 (Fig. 2) (Pedregosa et al. 2011).
2.5 SMOTE를 이용한 입력자료 구성
모형의 데이터 불균형을 해소하기 위해 대표적인 over-sampling 알고리즘 중 하나인 SMOTE를 이용하여 over-sampling을 수행하였다 (Lemaître et al. 2017). SMOTE는 KNN을 이용하여 소수 class의 데이터 수를 다수 class의 데이터 수와 동일하게 증가시켜 데이터 불균형을 해소하는 대표적인 over-sampling 방법이다. 입력자료 불균형의 해소가 모형 성능에 미치는 영향을 분석하기 위하여 실측 데이터를 사용하여 구축한 모형 (Model 1)과 SMOTE를 적용한 데이터를 입력자료로 사용한 모형 (Model 2)의 두 가지 모형을 구축하였다. 또한 입력자료 구성 비율의 차이에 따른 모형 성능 영향을 비교하기 위하여 상대적으로 자료수가 적은 class 3와 class 4의에 자료에 SMOTE를 적용하여 class 3와 4의 자료수가 원자료의 각 2배, 4배, 6배, 8배, 10배가 되도록 데이터를 구성하고 각 데이터 set을 이용하여 모형 Model S2, Model S4, Model S6, Model S8, Model S10을 구축하여 입력자료 구성에 따른 모형의 성능을 비교하였다. Model S10의 class 3은 가장 자료수가 많은 class 1과 동일한 945개의 자료로 모형을 구축하였다.
2.6 모형 성능 평가 방법
각 모형의 성능 평가는 분류모형의 성능 평가 지표 중 하나인 혼동행렬 (Confusion matrix)을 이용하여 성능을 평가하였다 (Table 1).
Table 1.
Confusion matrix
| Confusion Matrix | Predictive Values | ||
| Positive (P) | Negative (N) | ||
| Actual Values | Positive (P) | True Positive (TP) | False Negative (FN) |
| Negative (N) | False Positive (FP) | True Negative (TN) | |
Confusion matrix는 모형의 학습을 통해 나타난 예측 분류와 학습에 사용된 실제 분류의 분포를 행렬 형태로 나타낸 성능 평가 지표이며 예측의 정확도를 의미하는 True와 False 그리고 예측도를 의미하는 Positive와 Negative로 나누어져 있다. True Positive (TP)는 실측 값이 Positive이며 예측 값도 Positive인 경우, False Negative (FN)는 실측 값이 Positive이지만 예측 값이 Negative인 경우, False Positive (FP)는 실측 값이 Negative이지만 예측 값이 Positive인 경우, True Negative (TN)는 실측 값이 Negative이며 예측 값도 Negative인 경우를 의미한다.
Confusion matrix 값을 이용한 분류모형 성능 평가 방법인 정밀도 (Precision), 재현율 (Recall), F1-score를 확인하고 산술평균 (macro average)와 가중평균 (weighted average)를 계산하여 모형의 성능을 비교하였다. 정밀도는 모형이 예측 값 중 실측 값과 같은 값의 비율, 재현율은 실측 값 중 모형의 예측 값과 같은 값의 비율, F1-score는 정밀도와 재현율의 조화 평균을 의미한다. Macro average는 전체 class에서 계산한 값을 더한 후 전체 class 수로 나누어 평균을 계산하는 것을 의미하고 weighted average는 class에서 계산된 값에 전체 데이터 중 해당 class의 데이터의 비율을 가중하여 평균을 계산하는 것을 의미하기에 class 별 입력자료 수의 차이를 고려한 모형의 전체적인 성능을 비교할 수 있다 (Eqs. 1-3).
3. 결과 및 고찰
3.1 LGBM 모형 결과
본 연구에서는 입력자료를 하천의 T를 기준으로 4개의 class로 나누고 LightGBM을 이용한 다중 분류모형을 구축하였다. Model 1의 training 데이터의 수는 class 1이 945개, class 2가 763개, class 3은 95개, class 4는 25개로 class 1과 class 2에 비하여 class 3과 class 4의 데이터 수가 적어 데이터 불균형이 있음을 확인하였고 Model 2의 training 데이터 수는 모든 class가 동일하게 945개로 데이터 수가 늘어나 불균형이 해소된 것을 각 Model에 사용된 데이터 분포를 통해 확인하였다 (Fig. 3).
Model 1과 Model 2의 성능을 각각 Table 2와 Table 3에 제시하여 class 별 성능을 비교하였다. Model 1의 class 별 정밀도, 재현율, F1-score는 class 1과 class 2의 경우 각각 0.85, 0.82, 0.84와 0.71, 0.76, 0.73으로 분석되었고, class 3과 class 4의 경우 각각 0.26, 0.19, 0.22와 0.30, 0.60, 0.40으로 분석되었다. 모형의 전체적인 성능을 평가할 수 있는 macro average와 weighted average는 각각 0.53, 0.59, 0.55와 0.78, 0.77, 0.77로 분석되어 데이터 불균형으로 인하여 macro average가 weighted average에 비해 낮은 것으로 분석되었다. Model 2의 class 별 정밀도, 재현율, F1-score는 class 1과 class 2의 경우 0.88, 0.79, 0.83과 0.71, 0.76, 0.73으로 분석되었고, class 3과 class 4의 경우 각각 0.26, 0.38, 0.31과 0.25, 0.60, 0.35로 분석되었다. Macro average와 weighted average는 0.52, 0.63, 0.56과 0.78, 0.76, 0.77의 성능을 보였다. 소수 class에 대한 training 데이터의 수를 늘려주는 SMOTE로 인하여 상대적으로 데이터 수가 적은 class중 class 3의 성능이 크게 향상되어 macro average의 재현율의 성능이 좋아졌으나, 실측 값의 자료 수가 상대적으로 많은 다수 class인 경우 정밀도 값이 큰 차이가 없거나 소폭 하락하여 SMOTE 적용 이후 전체적인 모형의 정밀도가 소폭 하락한 것을 확인하였다.
Table 2.
Performance of model 1 using observation data
| Class | Precision | Recall | F1-score |
| Class 1 | 0.85 | 0.82 | 0.84 |
| Class 2 | 0.71 | 0.76 | 0.73 |
| Class 3 | 0.26 | 0.19 | 0.22 |
| Class 4 | 0.30 | 0.60 | 0.40 |
| Macro average | 0.53 | 0.59 | 0.55 |
| Weighted average | 0.78 | 0.77 | 0.77 |
Table 3.
Performance of model 2 using SMOTE data
| Class | Precision | Recall | F1-score |
| Class 1 | 0.88 | 0.79 | 0.83 |
| Class 2 | 0.71 | 0.76 | 0.73 |
| Class 3 | 0.26 | 0.38 | 0.31 |
| Class 4 | 0.25 | 0.60 | 0.35 |
| Macro average | 0.52 | 0.63 | 0.56 |
| Weighted average | 0.78 | 0.76 | 0.77 |
3.2 SMOTE 적용 비율에 따른 모형 성능 비교
데이터 불균형 해소를 위해 적용되는 SMOTE 알고리즘을 이용하여 데이터 구성 비율이 모형 성능에 미치는 영향을 비교하였다. 다양한 데이터 구성 비율에 따라 구축된 5개 모형인 Model S2, Model S4, Model S6, Model S8, Model S10의 class 별 데이터 수의 변화를 Table 4에 정리하였다. 또한 Fig. 4에 제시된 바와 같이 SMOTE의 적용 비율을 높임에 따라 소수 class의 자료 수가 증가하는 것을 시각적으로 확인할 수 있다.
Table 4.
Changes in the number of training data ratios using SMOTE
| Model | Class 1 | Class 2 | Class 3 | Class 4 |
| Model S2 | 945 | 945 | 190 | 50 |
| Model S4 | 945 | 945 | 380 | 100 |
| Model S6 | 945 | 945 | 570 | 150 |
| Model S8 | 945 | 945 | 760 | 200 |
| Model S10 | 945 | 945 | 945 | 250 |
SMOTE 알고리즘을 이용하여 다양한 데이터 구성 비율로 구축된 모형의 성능을 분석한 결과를 Table 5에 제시하고 모형 별 성능향상율을 계산하였다. 실측 값을 그대로 적용하여 구축된 Model 1을 기준으로 SMOTE를 이용하여 입력자료의 구성 비율을 다르게 하여 구축된 모형의 성능을 비교하였다. Model 1의 macro average는 정밀도, 재현율, F1-score가 각각 0.53, 0.59, 0.55로 분석되었다. Macro average의 개선율은 정밀도, 재현율, F1-score가 각각 Model S2는 5.7%, 6.8%, 5.5%, Model S4 9.4%, 10.2%, 9.1%로 모든 지표에서 성능이 개선된 것을 확인할 수 있었다. 또한 Model S6 1.9%, 3.4%, 0%, Model S8 –3.8%, -1.7%, -1.8%, Model S10 –1.9%, 5.1%, 0%로 산정되어 Model S6, S8, S10의 경우 정밀도는 감소하고, 재현율은 Model S8을 제외하고 전체적으로 개선되는 경향을 확인할 수 있었다. Weighted average의 경우 Model S2는 정밀도, 재현율, F1-score가 모두 1.3% 개선되었고, Model S4는 성능의 차이가 없는 것으로 분석되었다. Model S6, S8, S10은 성능의 변화가 없거나 다소 성능이 저하되는 것으로 확인되었다. Weighted average는 부여되는 가중치가 전체 데이터 수에 대한 해당 class의 데이터 수만큼 부여되기 때문에 모든 모형에서 유사한 성능을 보이는 것으로 판단된다. 전체 모형의 성능을 비교한 결과 Model S4의 macro average가 가장 높은 성능향상율을 보였으며, weighted average의 감소도 없어 가장 좋은 성능을 보이는 것으로 판단되었다 (Fig. 5).
Table 5.
Performance of models with SMOTE ratios
4. 결 론
본 연구는 LightGBM을 이용하여 하천의 탁도에 따라 4개의 class로 분류하고 예측하는 모형을 구축하고 입력자료를 일정한 비율로 SMOTE를 적용하여 모형의 예측성능을 비교하였다. 실측 데이터를 이용한 모형의 성능은 데이터 수가 충분한 class 1과 class 2는 상대적으로 우수한 성능을 보였지만, 데이터가 상대적으로 부족한 class 3과 class 4는 class 1과 class 2에 비해 낮은 성능을 보이는 것으로 분석되었다.
다수 class와 소수 class의 데이터 수 차이로 인해 발생하는 데이터 불균형의 해소를 위하여 SMOTE를 적용한 후 모형의 성능을 확인해본 결과 다수 class에서는 큰 차이가 없었지만, 소수 class인 class 3에서 재현율이 큰 폭으로 개선되어 전체적인 모형의 성능에 영향을 주는 것을 확인하였다.
본 연구에서는 또한 다양한 입력자료의 구성이 모형의 성능에 미치는 영향에 대한 분석을 위하여 입력자료의 구성 비율을 다르게 SMOTE를 적용하여 모형의 성능을 비교하였다. Class 1의 데이터 수와 약 10배의 차이가 있는 class 3의 데이터 수를 기준으로 다양한 데이터 구성비를 가진 모형의 성능을 비교한 결과 원자료의 4배의 자료를 적용한 Model S4가 가장 향상된 성능을 보이는 것을 확인하였다. 연구를 통해 모든 class에 동일하게 SMOTE를 적용하는 것보다 일정한 비율로 적용하는 것이 더 향상된 모형의 성능을 보이는 경우가 있다는 것을 확인할 수 있었으며 향후 입력자료 구성비의 변화가 머신러닝 모형 구성 주는 영향에 대한 지속적인 연구를 통해 데이터불균형의 해소를 통한 모형성능의 향상이 가능할 것으로 판단된다.