1. 서 론
2. 선형 평활화 알고리즘
2.1 Douglas-Peucker 알고리즘
2.2 Visvalingam-Whyatt 알고리즘
2.3 Bend-simplify 알고리즘
3. 연구방법 및 분석결과
3.1 연구방법
3.2 분석결과
4. 결 론
1. 서 론
하천내 친수지구는 주민들의 친수활동을 위한 공간을 계획적으로 관리하기 위하여 지정한 곳을 의미하며, 최근 도시지역 내 주민의 휴식과 레저를 위한 공간 부족을 해소하고, 하천이 제공하는 자연경관, 생태체험 등의 기회를 살려 지역의 활기를 높이는 역할이 강조되면서 친수지구 운영과 관리의 중요성이 점차 커지고 있다. 친수지구로 지정되면 하천관리청은 하천공사를 통해 광장, 자전거도로, 경관식재 등 하천을 이용한 기반을 확충하고, 이후에 지자체가 요구하는 이용객 편의시설, 저・문화시설 등의 설치 규제를 완화하여 지역의 건전한 하천이용을 지원하도록 하고 있다 (6). 이에 하천의 친수공간과 관련시설들이 효과적으로 조성 및 설치되고, 이후 꾸준히 관리될 수 있도록 하는 정책 및 제도적인 방안이 요구되고 있다 (Lee 2018).
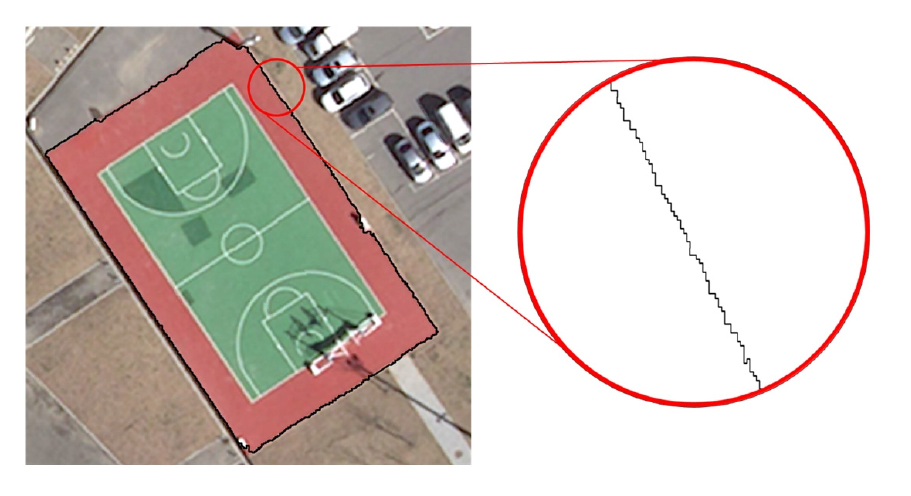
하천 친수공간의 관리를 위하여 선행되어야 할 부분은 대상 지구에 대한 정보 구축이다. 또한 시시때때로 변하는 하천시설 공간정보의 빠른 취득과 갱신은 하천의 친수시설 및 공간을 체계적으로 관리하기 위하여 가장 필수적인 요소이다. 현행의 친수공간에 대한 정보 구축은 해당 관리기관의 조사 등의 인적 조사 방식을 통하여 이루어지고 있으며, 이를 통한 데이터 수집에 많은 비용이 소모될 뿐만 아니라 DB의 최신화 부분에도 명확한 한계점이 존재한다. 따라서 하천 친수공원의 효율적인 관리를 위해서는 친수시설의 GIS 자료 및 DB구축의 자동화 작업이 필요하며, 이에 대한 대안으로 드론영상이나 항공영상을 활용한 객체기반 분류 방법이 국토의 3차원 공간정보를 획득할 수 있는 효율적 수단으로 주목받고 있다 (Kim 2019). 다만 영상처리시에 처리 대상이 되는 영상은 Fig. 1과 같이 본질적으로 울퉁불퉁한 경계로 이루어져 있으며 또한 다양한 경계 노이즈(boundary noise)를 포함하고 있다 (Kim 1999). 추출된 윤곽선에 포함된 노이즈를 제거하기 위해서는 윤곽선의 선형 평활화 작업이 필요하며 공간정보 획득 시에는 그 표현 방법에 대한 법칙 및 방법들을 포함하고, 이러한 방법들을 수동으로 적용하기에는 많은 어려움이 따르게 된다. 이러한 어려움을 극복하기 위하여 여러가지 자동화 방법들이 개발되었고, 그 중 현재까지 가장 널리 연구되고 활용되어지고 있는 방법은 선형 평활화 방법이라고 할 수 있다. 선형 평활화 방법은 지도 일반화 기술 중에서 가장 핵심이라고 할 수 있는 방법으로 모든 선형 객체에 대하여 불필요한 절점의 삭제 또는 중요한 영역의 보존 등의 방식으로 객체를 평활화 시키는 방법이다 (Lee et al. 2012).
선형 평활화 방법에 대한 기존 연구들은 단일 알고리즘에 대하여 임계값을 조절하고 그에 따른 성능평가에 대한 연구가 주를 이루었다 (Shahriari and tao 2002, Cheung et al 2006, Shi and Cheng 2006). Lee et al. (2012)은 건물, 하천, 도로의 형상을 추출하고 여러 알고리즘에 대해 임계값의 조절에 따른 성능평가에 대한 연구를 진행하였다. Park et al. (2008)은 CAD 데이터에서 GIS 정보를 추출하기 위한 건물외곽선의 평활화 기법을 비교하였다. 이와 같이 객체 추출을 위한 선형 평활화 방법에 대한 연구가 꾸준히 진행되어 오고 있지만 건물 및 도로 등의 구조물에 대한 분석이 주를 이루고 있으며 여러가지 기하학적 형상을 가진 공간에 대한 연구는 부족한 실정이다. 따라서, 본 연구에서는 여러 평활화 알고리즘들의 임계값을 변화시키면서 각 기하학적 형상을 가진 친수시설물 추출객체에 알고리즘을 적용시키고, 그 결과를 분석하고자 하였다. 이를 위하여 현재까지 가장 널리 사용되는 Douglas-Peucker, Visvalingam-Whyatt, Bend-simplify 알고리즘을 선택하여 평활화 결과물에 대한 면적을 측정하여 비교하였고, 분류된 객체의 면적오차를 비교하여 기하학적 형상별 분석에 가장 적합한 알고리즘 및 그에 따른 임계값을 선정하고자 하였다.
2. 선형 평활화 알고리즘
선형 평활화 과정에는 여러가지 알고리즘에 사용되고 있으며, 평활화 알고리즘은 평활화 과정에서 임계값의 사용여부, 평활화 혹은 원활화 여부 등의 특성에 따라 여러 가지 기준에서 구분될 수 있다.
2.1 Douglas-Peucker 알고리즘
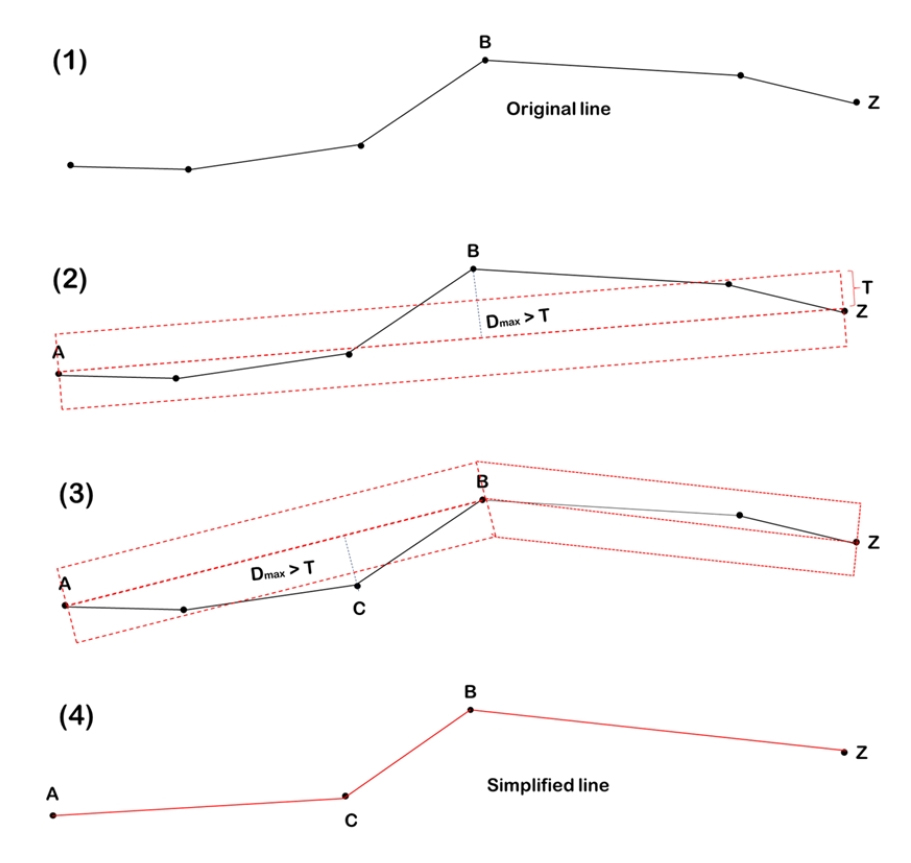
Douglas-Peucker 알고리즘은 복잡한 형태의 선 구조를 평활화시키는 선형 평활화 기법이다 (Douglas et al. 2012). 이 알고리즘은 1973년 발표되어 현재까지 가장 널리 사용되고 있으며, 오브젝트를 이루는 여러 좌표점의 개수를 허용 오차에 따라 설정된 임계값과의 비교를 통해 줄이는 방식이다. 즉, 임계 값과의 비교를 통해 비 중요 좌표점을 없애는 방식이다.
Douglas-Peucker 알고리즘의 수행 단계 (Fig. 1)는 다음과 같다. 우선 평활화할 오브젝트의 시작점과 끝점을 연결한 선과 각 좌표점들이 수직으로 연결되는 수선의 길이 중 임계값을 벗어나는 최대 수선의 길이 Dmax를 찾는다. 그리고 이 좌표점을 새로운 중간점으로 설정하고 시작점과 끝 점과 연결함으로써 오브젝트를 분할하고, 임계값을 벗어나는 수선의 길이를 가지는 좌표점이 존재하지 않게 되면, 분할된 오브젝트 내의 좌표점을 제거하는 과정을 재귀적으로 반복 수행한다. 시작점, 끝점, 임계값에 따라 남겨진 분할점들만으로 평활화된 오브젝트가 만들어진다. 이렇게 생성된 오브젝트들은 원래 오브젝트와 비교하였을 때 시작점과 끝점만 동일할 뿐, 오브젝트를 구성하는 좌표 점들의 개수와 좌표 데이터는 다르게 된다. 하지만 Douglas-Peucker 알고리즘은 사용자가 설정하는 임계값에 따라 좌표점 압축 수행결과가 크게 달라진다. 또한 Douglas-Peucker 알고리즘은 오브젝트를 구성하는 좌표점을 직접 제거해 버리기 때문에 오브젝트의 형상이 Douglas-Peucker 알고리즘 수행전의 원래 오브젝트와 비교하여 달라질 수도 있는 단점이 있다.
2.2 Visvalingam-Whyatt 알고리즘
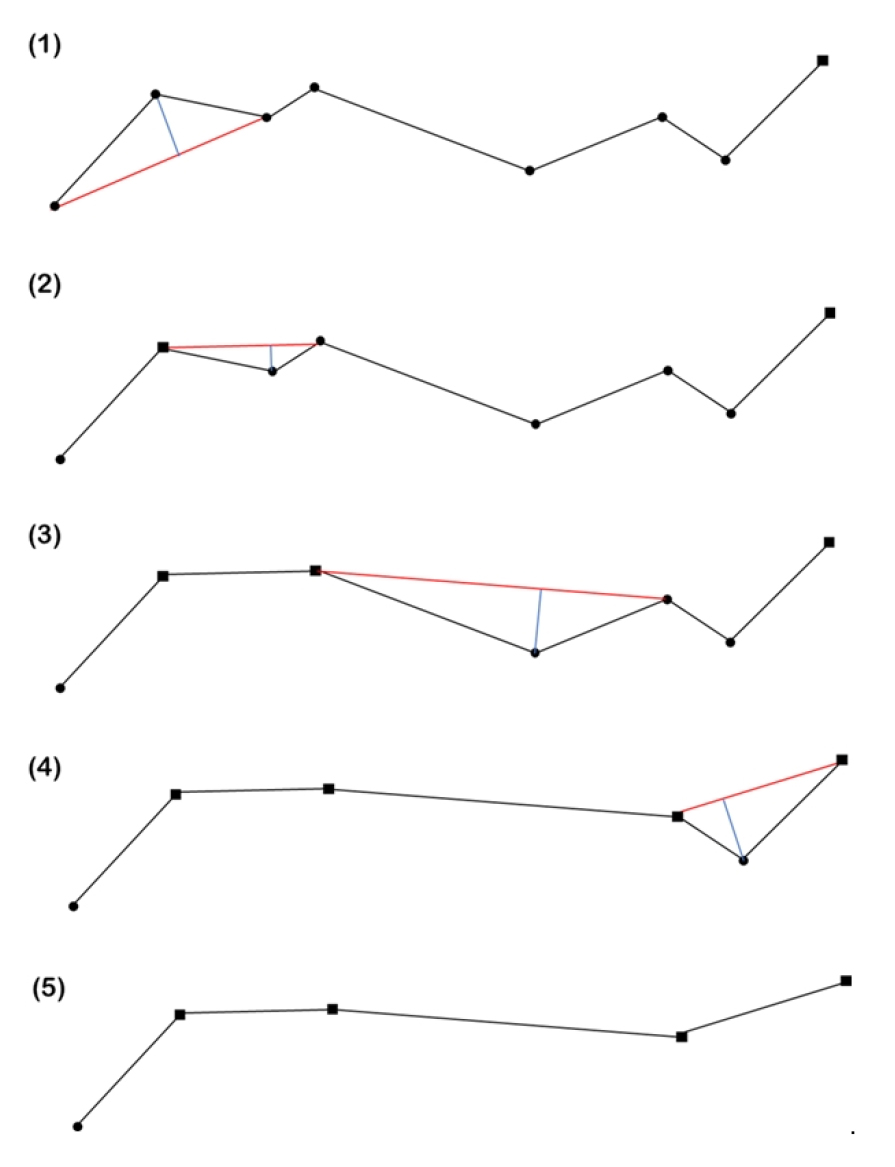
Visvalingam-Whyatt 알고리즘은 대상 선형 전체에 대 해서 인접한 세 점으로 구성된 삼각형의 면적인 유효면 적을 계산하게 된다 (Visvalingam and Whyatt 1993). Visvalingam-Whyat 알고리즘의 수행 단계 (Fig. 3)는 다음과 같다. 우선 시작점과 끝점을 제외한 꼭지점에 대해 이웃한 두 꼭지점를 연결하여 삼각형을 형성한다. 이 삼각형의 면적을 해당 꼭지점의 ‘유효면적 (effective area)’으로 규정한다. 그리고 유효면적이 가장 작은 삼각형의 해당 꼭지점을 ‘현행포인트 (current point)’로 규정하고, 그것을 제거하고, 제거된 꼭지점의 양쪽에 위치한 두 꼭지점 각각에 대하여 삼각형을 구성하고 유효면적을 계산하여 비교한다. 이와같은 과정을 시작점과 끝점만 남을 때까지 반복하고 임계 유효면적을 설정하면 각 단계의 최소 유효면적과 비교하여 전자보다 후자가 크면 반복을 종료하여 평활화 오브젝트를 만든다 (Kim and Lee 2021).
2.3 Bend-simplify 알고리즘
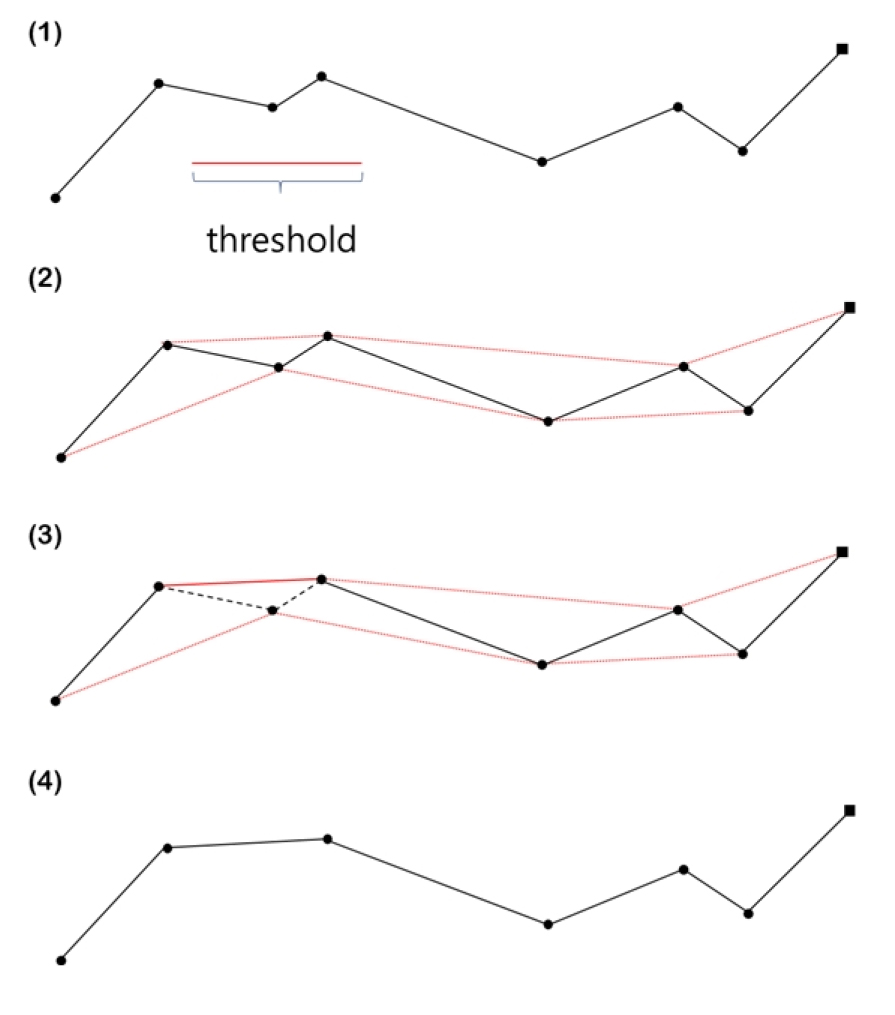
Bend-simplify 알고리즘은 Visvaligam-Whyatt 알고리즘과 마찬가지로 영역을 기반으로 한 평활화 알고리즘이다 (Wang et al. 1998). 이 알고리즘은 선형을 변곡점 단위로 나눠지는 Bend 단위로 분할한 후, 각각의 Bend들의 특징을 파악하고, 불필요한 Bend의 경우, 그 Bend를 제거하는 방식이다. Bend-simplify 알고리즘의 수행 단계 (Fig. 4)는 다음과 같다. 우선 Bend 단위로 선형을 분할하기 위해서는 각 점에서 두 선분이 이루는 각도를 계산하여, 이 각도가 같은 방향성을 보이는 선형을 하나의 Bend로 인식한다. Bend 단위를 인식한 후에는, 각 Bend의 밑선의 길이를 계산하고, 이 밑선의 길이가 주어진 임계값 보다 작을 경우 이 Bend를 제거한다. Bend-simplify 알고리즘은 해안선 조사 및 자료 처리 등에 관한 업무규정 제41조 (축척이 다른 도면 제작에 필요한 해안선의 편집 등)에 해안선의 편집방법으로 명시되어 있는 알고리즘이다.
3. 연구방법 및 분석결과
3.1 연구방법
본 연구에서는 부산 대저, 부산 삼락, 서울 반포, 서울 이촌 친수지구의 항공영상으로부터 LSMS (Large- Scale Mean Shift) 기법을 이용하여 친수시설을 객체분류하고 분류된 친수시설의 객체를 Fig. 5와 같이 각 기하학적 형상별로 분류하여 비교 데이터로 사용하였다.
본 연구에서는 친수시설 객체에 선형 평활화 알고리즘 (Douglas-Peucker, Visvalingam-Whyatt, Bend- simplify)에 대하여 각각 5단계로 임계값을 조절하면서 사각형, 삼각형, 타원형으로 분류된 친수시설 형상에 각 객체마다 알고리즘을 적용하였다. 임계값 조절에 있어서, 각 알고리즘마다 동일한 임계값이 미치는 민감도는 다를수 있기 때문에 평활화된 객체가 최대한 동일한 수준의 결과가 나올 수 있도록 시산법을 통하여 임계값을 결정하였다. 각 알고리즘의 임계값의 설정은, Douglas-Peucker의 경우 오차량 자체가 임계값의 영향을 크게 받기 때문에 1 m로부터 1 m간격으로 5단계로 설정하였다. Visvalingam-Whyatt 알고리즘은, 1 m2부터 1 m2단위로 설정하여 분석하였고, Bend-simplify 알고리즘에서도 1 m단위의 임계값으로 분석을 수행하였다. 결과 비교는 사각형, 삼각형, 타원형의 객체에 대하여 3가지 알고리즘을 적용시키고 임계값을 변화시키고 그 결과물에 대하여 면적오차의 비교를 수행하였다. 면적오차는 GIS 툴을 이용하여 실제 친수시설의 면적과 추출한 객체의 면적의 차이를 비교하여 각 기하학적 특성에 따른 알고리즘 별 오차량의 증가를 분석하였다.
3.2 분석결과
상기의 분석과정을 통하여 산출한 데이터를 그래프화 하여 비교 정리하였다. 각 알고리즘에 대하여 사각형, 삼각형, 타원형의 3가지 기하학적 형상에 대한 면적오차를 측정하여 비교하였다.
3.2.1 사각형 형상
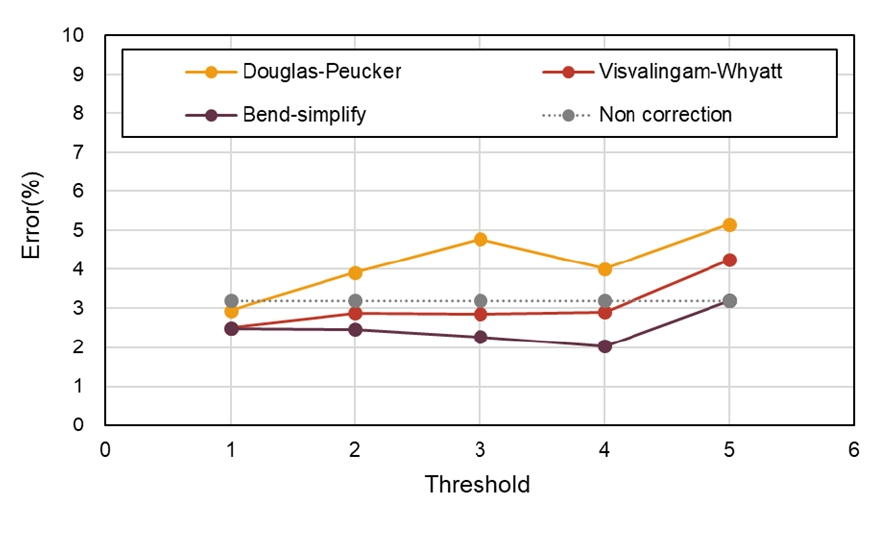
사각형 형상에 대한 오차 분석결과 3가지 선형 평활화 알고리즘의 오차값의 분포에서 Bend-simplify 알고리즘의 오차가 가장 낮게 나타났다 (Fig. 6). Bend-simplify 알고리즘의 경우 모든 임계값의 범위에서 가장 작은 오차가 나타났다. 또한 최소 오차는 임계값 4에서 2.03%, 최대 오차는 임계값 5에서 3.20%으로 나타났다. 가장 높은 오차를 나타낸 알고리즘은 Douglas-Peucker 알고리즘이었고 최대 오차는 임계값 5에서 5.16%로 나타났다. 또한 선형 평활화 알고리즘을 적용하지 않고 LSMS 기법만을 적용하여 생성한 형상과의 오차는 3.23%로 나타났다. 이상의 결과로 사각형 형상에 대한 최적 선형 평활화 알고리즘은 Bend-simplify이라고 판단되며 가장 많이 사용되는 Douglas-Peucker 알고리즘의 경우 선형 평활화 알고리즘 적용 전과 비교하여 오차가 더 큰 것으로 나타났다.
3.2.2 삼각형 형상
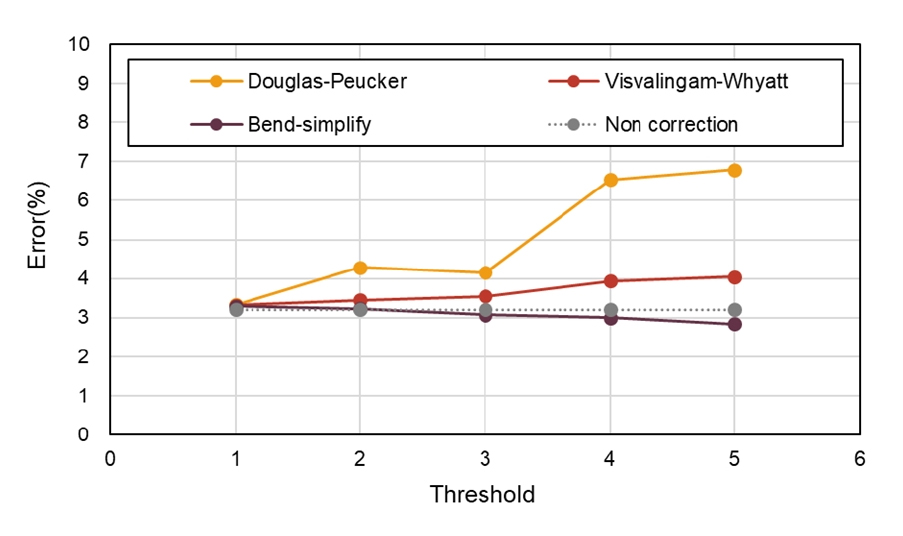
삼각형 형상에 대한 오차 분석결과 3가지 선형 평활화 알고리즘의 오차값의 분포에서 사각형 형상과 동일하게 Bend-simplify 알고리즘의 오차가 가장 낮게 나타났다 (Fig. 7). Bend-simplify 알고리즘의 경우 모든 임계값의 범위에서 가장 작은 오차가 나타났다. 또한 최소 오차는 임계값 5에서 2.83%, 최대오차의 크기는 사각형 형상과는 반대로 임계값이 커짐에 따라 점점 작아지며, 임계값 1에서 3.29%로 나타났다. 가장 높은 오차를 보인 알고리즘은 Douglas-Peucker 알고리즘이었고, 최대 오차는 임계값 5에서 6.79%로 나타났다. 또한 선형 평활화 알고리즘을 적용하지 않고 LSMS 기법만을 적용하여 생성한 형상과의 오차는 3.21%로 나타났다. 이상의 결과로 삼각형 형상에 대한 최적 선형 평활화 알고리즘은 Bend-simplify이라고 판단되며 삼각형 형상에서는 Visvalingam-Whyatt과 Douglas-Peucker 알고리즘은 선형 평활화 알고리즘 적용 전과 비교하여 오차가 더 큰 것으로 나타났다.
3.2.3 타원형 형상
타원형 형상에 대한 오차 분석결과 사각형과 삼각형 형상과는 달리 내부의 끼인각이 존재하지 않는 형상으로 선형 평활화 기법의 결과도 다른 두가지 형상과 다른 결과를 나타냈다 (Fig. 8). 오차 분석결과 3가지 선형 평활화 알고리즘의 오차값의 분포에서 임계값 1 - 2에서는 Visvalingam-Whyatt 알고리즘의 오차가 가장 작게 나타났으나, 임계값 3이후부터는 다시 Bend-simplify 알고리즘의 오차가 가장 낮게 나타났다. 그러나 임계값 1 - 2의 경우에 Visvalingam-Whyatt 알고리즘과 Bend-simplify 알고리즘의 오차 차이는 약 0.07%로 굉장히 낮은 차이를 보였다. 또한 선형 평활화 알고리즘을 적용하지 않고 LSMS 기법만을 적용하여 생성된 형상과의 오차는 1.10%로 확인하였다. 최대 오차는 사각형과 삼각형 형상과 비교하여 1.50%이하의 낮게 나타났는데 그 이유는 끼인각이 존재하지 않아 생기는 현상으로 판단된다. 가장 높은 오차를 보인 알고리즘은 Douglas-Peucker 알고리즘이었고 최대 오차는 임계값 5에서 1.33%으로 나타났다. 이와 같은 결과로 보아 타원형 형상에서 가장 적합한 선형 평활화 알고리즘은 Bend-simplify이라고 볼 수 있다.
4. 결 론
본 연구에서는 하천 친수공원의 효율적인 관리를 위한 친수시설의 GIS 자료 및 DB구축에 있어서 항공영상을 활용한 친수시설의 객체추출 정확도를 향상시키고자 객체추출한 사각형, 삼각형, 타원형의 실제 친수시설 형상에 대하여 선형 평활화 알고리즘을 적용한 결과에 대한 정량적인 평가를 통하여 각 기하학적 친수시설물 형상에 대한 최적의 선형 평활화 알고리즘을 선정하고자 하였다. 본 연구를 통해 얻은 결론은 다음과 같다.
우선 사각형 형상의 친수시설에 가장 적합한 선형 평활화 알고리즘은 Bend-simplify 알고리즘이었으며 오차 범위는 2.03% - 3.20%로 나타났고, 삼각형 형상의 친수시설에 가장 적합한 선형 평활화 알고리즘은 Bend-simplify 알고리즘이었으며 오차 범위는 사각형 형상과 비슷하게 2.83% - 3.29%로 나타났으며 타원형 형상의 친수시설에 가장 적합한 선형 평활화 알고리즘은 Bend-simplify 알고리즘이었으며 오차 범위는 세가지 형상 중 가장 낮은 0.40% - 1.17%로 나타났다. 이는 다른 두형상에 비해 끼인각이 없는 타원형 형상에서 평활화시키는 선분이 적기 때문이라고 판단된다.
이와 같이 객체추출한 친수시설의 모든 형상에서 공통적으로 Bend-simplify 알고리즘이 가장 낮은 오차율을 보였다. 따라서 친수시설의 객체분류 후에 선형 평활화 작업을 수행함에 있어 Bend-simplify 알고리즘을 사용하는 것을 추천하며 친수시설의 형상에 따라 임계값을 조절하여 적정 형상을 추출하는 것이 적절할 것으로 판단된다.
마지막으로 본 연구에서는 친수시설의 형상을 사각형, 삼각형, 타원형으로 3가지 종류에 대하여 분석하였고, 실제 친수지구에는 더욱 다양한 형상의 친수시설이 존재하므로 향후 원형이나 팔각형 등의 좀 더 다양한 형상의 친수시설 형상에 대한 연구가 필요할 것으로 판단된다.