1. 서 론
2. 연구 방법
2.1 연구 대상 유역
2.2 물리적 기반 모형의 적용
2.3 물리적 기반 모형의 보정 및 검증 방법
2.4 Gamma Test
3. 결과 및 고찰
3.1 물리적 기반 모형의 보정 및 검증결과
3.2 데이터 기반 수질 예측 모형 구성을 위한 불확실성 분석
4. 결 론
1. 서 론
최근 유역관리를 위하여 빅데이터 기반의 분석 기법이 적용되고 있다. 이 중 예측 분석 (Predictive Analytics)은 과거의 패턴 식별을 통한 예측 기능으로 과거의 관측 자료 또는 물리적 기반 모형의 결과를 학습시켜 데이터 기반 모형 (Data-driven model)을 개발하는 것으로 홍수, 수질오염 예측 등 물재해에 대한 사전관리를 위해 적용이 가능하다 (Poul et al. 2019). 특히 수자원 분야에서 다양한 데이터 분석 및 기계학습의 방법론이 적용되고 있으며 데이터 기반 모형은 수문학의 기본인 물리학적 프로세스를 직접 고려하지 않고 과거의 데이터를 사용한다는 특징이 있다 (Keum et al. 2019). 수질의 경우, 오염원의 불확실성과 비선형적 관계로 인해 데이터 기반 모형을 활용한 수질 예측이 새로운 모델링 툴로 평가받고 있으나 대량의 수질자료 간 상호연관성과 의도적으로 지나치게 단순화된 가정 등이 존재하기 때문에 다양한 유형의 불확실성과 모호성에 대해 지적된 바 있다 (Kim and Seo 2015). 데이터 기반 모형인 ANFIS (Adaptive Neuro-Fuzzy Inference System)의 경우 각 입력자료의 규칙이 3개라고 하면 퍼지이론에 따라 총 규칙의 수는 3n개가 된다. 입력변수가 증가할수록 이와 비례하여 모형의 정확도가 증가하는 것은 아니며 퍼지 규칙수가 기하급수적으로 증가함으로써 모의시간이 길어지게 되는 단점이 있다 (NDMI 2018). 따라서 예측결과의 정확도를 높이면서 모의시간 또한 적정하게 단축시킬 수 있는 입력자료 조합을 선정하기 위한 입력변수와 출력변수 간의 상관관계 분석은 필수적인 선행 단계라고 할 수 있으며, 분석방법으로는 주성분 분석, 군집분석, AIC, BIC 분석, K-fold Cross Validation, Gamma Test 등이 있다.
데이터 기반의 수질 예측 모형을 구축한 선행연구 사례를 보면 대부분 월단위 이상의 수질 관측자료를 입력자료로 구성하였다 (Faruk 2010, Najah et al. 2013, Sarkar and Pandey 2015, Khadr and Elshemy 2017). 국내 수질측정망 중 가장 많은 자료의 수로 공인된 수질을 제공하고 있는 것은 8일 간격의 총량측정망 자료라고 할 수 있는데 해당 자료만으로 데이터 기반 모형을 구축하기에는 자료의 개수가 부족하며 특정 유량구간에 수질 측정이 편중되어 있을 경우 해당 유량구간의 수질영향이 과다하게 반영되는 결과를 초래하는 한계점을 가지고 있다고 보고된 바 있다 (Park and Oh 2012, MOE 2015, Lee et al. 2018).
본 연구에서는 비선형성 특성을 가지는 수질 예측 모형의 입력자료를 최대한 확보하고자 지형, 오염원, 기상, 수문 등 유역환경조건을 반영하고 실제 관측자료로부터 보검증을 완료한 물리적 기반 모형으로부터 도출하였으며, 일단위로 확보된 입력자료에 대한 사전 불확실성 점검과 함께 신뢰도 향상을 위하여 Gamma Test를 수행하여 최적의 자료 조합을 선정하고자 한다. Gamma Test는 Stefánsson et al. (1997)에 의해 소개된 이론으로 NH3 -N, BOD 등의 수질 예측을 위한 모형 구축 시 핵심 입력인자 조합 선정을 위해 적용된 바 있다 (Chang et al. 2015, Lee and Kim 2021). 연구대상유역은 우리나라 수도권 시민의 상수원인 팔당댐 유역으로 수질예측을 위한 목표지점은 EFDC (Environmental Fluid Dynamic Code), 팔당댐으로 유입되는 주요 하천별 수질은 HSPF (Hydrological Simulation Program – Fortran)모형을 적용하였다. 즉, 목표지점 (팔당댐)의 수질과 총 9개의 유입하천별 수질에 대하여 수질항목별 Gamma Test의 다양한 적용 결과를 고찰하였다.
2. 연구 방법
2.1 연구 대상 유역
본 연구의 대상 유역은 한강 대권역 내 충주댐하류, 섬강, 남한강하류, 의암댐, 홍천강, 팔당댐, 경안천, 한강잠실 등 9개 중권역을 포함하는 약 2,550만 명 수도권 시민의 상수원인 팔당댐의 영향권이다. 팔당댐은 국내 최대 규모의 취수원으로 수질측면에서 매우 큰 관심을 받고 있으며, 수질보전을 위한 엄격한 규제로 인해 목표수질 달성여부 또는 수질변화가 매우 중요한 유역이다 (Kim and Lee 2019).
팔당댐은 23,800 km2의 넓은 유역면적을 가진 데 비하여 수면적이 36.2 km2이고, 유효 저수량이 2억 4,400만 톤으로 물그릇이 작아 체류시간이 평균 5 - 6일, 평균 수심 약 6.5 m로 하천형 인공호로서 하천 기준인 BOD가 목표수질 중 하나로 평가되고 있다 (Kim et al. 2009).
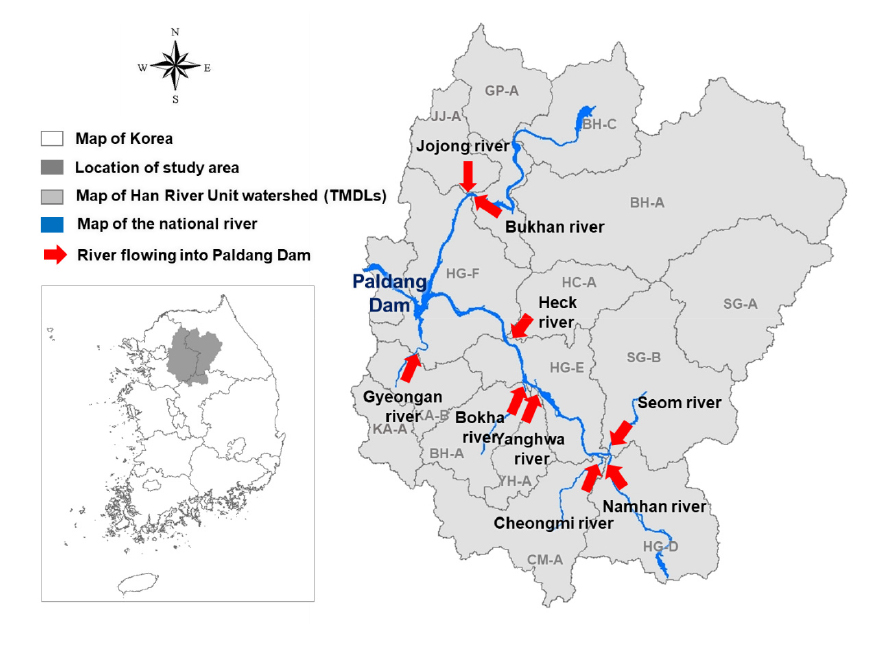
본 연구에서 수질예측 목표지점으로 설정한 팔당댐2지점은 수도권 광역상수도 취수구 인근에 위치하고 있으며 우리나라 물환경분야의 최상위계획에서 관리하고 있는 목표기준은 Ⅰa등급이다. 해당 지점은 Fig. 1과 같이 남한강 (한강D), 북한강 (북한D)을 비롯한 경안천 (경안B), 조종천 (조종A), 양화천 (양화A), 청미천 (청미A), 섬강 (섬강B), 흑천 (흑천A), 복하천 (복하A) 등 많은 유입하천의 영향을 받고 있다.
2.2 물리적 기반 모형의 적용
본 연구에서 다양한 유량조건에서의 일단위 수질을 생산하기 위해 물리적 기반 모형을 적용하였다. 먼저 수질예측의 목표지점으로 설정한 팔당댐2지점의 경우 호소모형인 EFDC 모형을 구축᛫구동하였으며, 팔당댐으로 유입되는 주요 하천별 수질을 모의하기 위해 유역모형인 HSPF 모형을 적용하였다. 또한 EFDC 모형 구축 시 HSPF 모형의 모의자료를 초기 및 경계조건으로 입력하여 구동하였다.
HSPF 모형은 강우로 인한 비점오염물질 유출과정을 하천 내에서의 수리학적 현상, 퇴적물, 화학물질의 상호작용과 결합시켜 모의할 수 있는 유역모델과 수질모델이 결합된 형태를 가진 유역유출모델이다 (U.S. EPA 2001). HSPF 모형의 사용을 위해 GIS 기반으로 방대한 자료를 관리하고 다양한 모델들을 지원해주는 통합관리시스템인 BASINS를 이용하여 기본정보를 입력하였다. 먼저 DEM으로부터 Flow Direction과 Flow Accumulation을 계산하여 하천망을 생성시킨 후 유역의 출구지점을 outlet으로 지정하여 분할하였으며, 토지피복도는 Urban or Built-up land, Wetland, Agricultural land, Forest Land, Pasture Land, Barren Land, Water 등 7개 항목으로 분류한 후, 모형 내 Landuse and Soil Definition Utility를 이용하여 분할된 소유역에 대한 각각의 토지이용 정보를 추출하였다. 기상자료는 강수량, 기온, 이슬점온도, 운량, 일사량, 풍속, 증발산량 등 7개 항목의 시간단위 관측값을 입력한 후 WDMUtil 내의 Disaggregate Fuctions 중 Evapotranspiration을 활용하여 증발산량을 생성하였다. 점오염부하량 자료는 2008 - 2018년의 오염원 조사자료로부터 오염부하량을 산정하여 입력하였으며, 일평균 방류량이 500 m3이상인 공공하수처리시설은 일별 방류량과 방류수질 (BOD, SS, T-N, T-P) 자료를 수집하여 입력하였다. 댐 방류량, 광역 취수자료는 일단위, 지방상수도는 월단위의 취수자료를 조사하여 입력하였다.
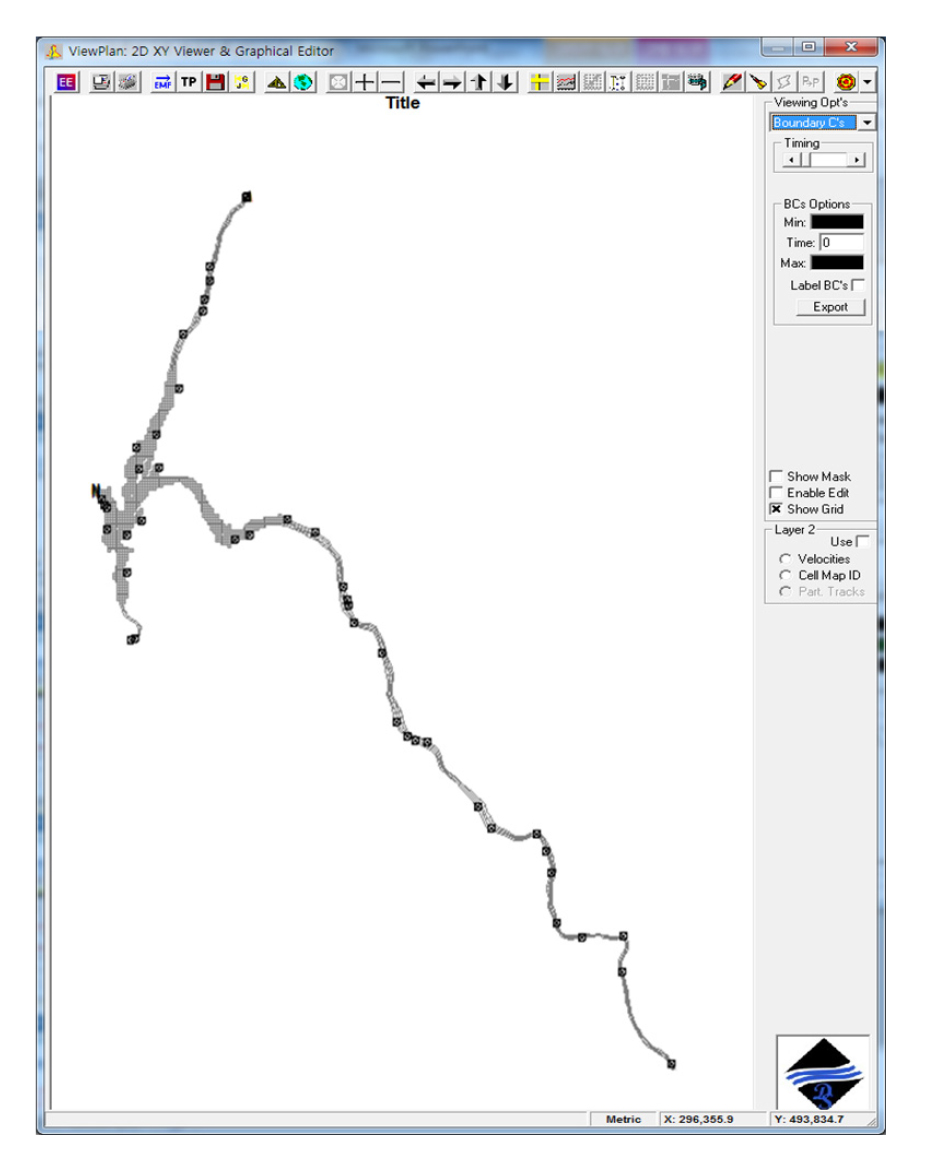
EFDC 모형은 연안, 하구, 호소, 습지, 저수지 등 유동 및 물질수송을 모의하는 3차원 수치모델로서 미국 VIMS (Virginia Institute of Marine Science)에서 개발되었다 (Tetra Tech, Inc. 2007). 팔당댐 유역의 EFDC 모형 구성은 북한강, 남한강, 경안천에서 팔당댐까지를 대상으로 하였다. 격자구성을 위해 필요한 지형자료는 한강수계 횡단면도를 AutoCAD에 적용하여 구성하였으며, 격자 크기가 작아질수록 대상 유역의 격자수가 많아져 모의시간이 길어지기 때문에 팔당댐은 200 m × 200 m 크기의 cell로 구성 (Cartesian Coordinate)하고 그 외의 하천은 Orthogonal Curvilinear Coordinate 방법을 사용하여 수평방향으로 2,700개의 격자를 구성하였다. HSPF 모형에서 나오는 유량 및 수질 결과파일을 EFDC 모형으로 입력하기 위한 경계지점은 40개로 지정하였다 (Fig. 2).
2.3 물리적 기반 모형의 보정 및 검증 방법
HSPF 모형의 보정 및 검증에 사용한 관측자료는 먼저 유량은 문막교, 원부교, 여주대교, 흥천대교, 흑천교, 양평교, 가평교, 청평교, 경안교, 팔당대교 등 10개의 수위관측소 자료를 이용하였다. 수질은 한강물환경연구소에서 각 총량관리 단위유역 말단에서 측정한 연간 약 40회의 수질자료를 활용하였다. EFDC 모형의 경우 팔당댐에서 수위보정을 수행하였으며 수질은 팔당댐 2지점에서 관측된 자료를 활용하였다 (Fig. 3). HSPF, EFDC 모형의 보정과 검증기간은 각각 2015 - 2018년, 2011 - 2014년도 자료를 이용하였다.
유량의 보정 및 검증 결과에 대한 적정성을 평가하기 위하여 결정계수 (R2)와 % difference를 산정하였으며 Tables 1 and 2의 기준을 근거로 판단하였다. 수위의 경우, % difference와 관측값과 모의값의 평균값을 비교하였다. 수질은 수질항목별로 관측값과 모의값의 평균값을 제시하였으며 % difference, RMSE (Root Mean Square Error)를 산정하여 관측값에 대한 수질 보정 및 검증 결과의 적정성을 평가하였다.
Pi : predicted values, Oi : observed values
Table 1.
The General calibration/validation target or tolerance for HSPF application (Donigian 2000)
| Criteria | Very good | Good | Fair | Poor |
| R2 | > 0.8 | 0.8 – 0.7 | 0.7 – 0.6 | < 0.6 |
Table 2.
The % difference value range for Model performance (Donigian 2000)
| Constituent | Very good | Good | Fair |
| Hydrology / Flow | < 10 | 10 - 15 | 15 - 25 |
| Water Quality | < 15 | 15 - 25 | 25 - 35 |
2.4 Gamma Test
Gamma Test는 연속적인 비선형 기법을 사용하여 데이터를 모델링 할 때 산정되는 최소 평균제곱오차를 추정하는 기법으로 최초로 Stefánsson et al. (1997) 의해 발표된 후, 많은 연구자들에 의해 기법이 발전되고 구체적으로 정립되었다 (Keum et al. 2019). Gamma Test를 위한 기본적인 개념은 비선형 해석을 이용한 기존의 자료 전처리를 위한 분석방법과는 차별성이 있다. Eq. 2와 같이 분석 대상 자료가 있다는 가정 하에 분석을 실시한다.
여기서, 입력 벡터 xi∈Rn는 폐집합 C∈Rn에 한정된 벡터이며, 일반적인 모형의 결과 또는 종속변수에 해당되는 출력값 yi ∈ Rn는 스칼라이다. 벡터 x값들은 출력값 y에 영향을 주며 예측을 위한 입력값으로 사용할 수 있는 독립변수이다. x와 y관계에 대한 기본적인 가정은 다음과 같다.
여기서, f는 지수 평활법 함수이고 y은 노이즈를 나타내는 확률 변수이다. Eq. 3에서 x값은 입력자료, y값은 예측되는 결과를 나타낼 수 있다. Gamma Test는 각 벡터 xi (1≤i ≤M)에 대한 k번째 (1≤i ≤p) 가장 가까운 변수 N[i,k]를 기반으로 비선형 분석을 실시한다. 각각의 입력자료 x에 대해서 k개의 최근접 이웃자료와의 평균 제곱근거리를 산정하게 된다. 이에 대한 수식은 Eq. 4와 같다. 독립변수 x에 대응되는 결과 (또는 목표)값이 되는 y에 대해서도 동일한 방식으로 k개의 최근접 이웃자료와의 평균 제곱근거리를 산정하게 된다 (Eq. 5).
각 변수들에 대한 최근접 이웃자료와의 물리적 거리의 관계를 산정하였을 때에, 자료 양과 동일한 수만큼의 δ와 γ의 값들이 생성되게 되며, 두 값을 통하여 τ을 산정하기 위한 회귀식을 생성하게 된다. 이를 통하여 산정된 감마 통계량 τ는 지수 평활법 데이터 모형에 의해 설명될 수 없는 인공신경망 모형의 결과값에 대한 분산의 추정치이다 (Eq. 6).
산정된 τ는 특정 입력 자료조합에 따른 불확실도 Vratio지표를 산정할 때에 사용된다. Eq. 7에서 σ2(y)는 출력 y의 분산이며, 이는 출력이 부드럽고 신뢰성 있게 모델링 될 수 있는지에 대하여 출력 범위와 독립적으로 예측력에 대한 판단이 가능하도록 만들어준다. 0에 가까운 Vratio는 주어진 출력 y의 높은 예측 가능성을 나타낸다. 위의 과정을 통하여 Gamma Test는 예상 노이즈 분산을 근사하는 평균제곱오차로 모델을 구축하는 데 필요한 데이터의 양을 결정하는데 도움을 줄 수 있다 (Rauf et al. 2016).
3. 결과 및 고찰
3.1 물리적 기반 모형의 보정 및 검증결과
3.1.1 유량 및 수위
모형의 보정은 모형의 초기조건과 매개변수를 유역의 실제 여건에 맞게 환경을 구성하는 과정으로 모의된 값과 관측된 값이 가장 근접할 때의 매개변수 값을 추정하는 것이다 (Lee 2013). 보정기간 동안 시행착오법으로 HSPF, EFDC 모형의 모의 결과가 관측값과 최대한 근접하도록 하였으며 검증을 수행함으로써 보정기간에 맞춰진 모형 매개변수들의 타당성을 검토하였다.
먼저 HSPF 모형에서 유량의 보정 및 검증기간은 각각 2015 - 2018년, 2011 - 2014년으로 4개년씩 지정하여 R2, %difference값을 산정하였으며, Table 3에서 보는 바와 같이 10개의 수위관측소에 모두 Very good으로 모형의 모의치가 실측치를 매우 잘 반영하는 것으로 나타났다. 강우 시의 첨두값이 대부분 관측값보다 약간 작게 모의되어 저·갈수기의 유량을 보다 잘 재현하는 것으로 나타났다. Table 4는 EFDC 모형에서 팔당댐 수위에 대해 보정 및 검증한 결과로 관측값과 모의값의 평균, %difference값을 산정한 것으로 Very good으로 평가되었으며 여름철 수위가 급격하게 증가하거나 감소하는 일부를 제외하고 모의값과 실측값이 적절히 일치하였다.
Table 3.
The HSPF model statistical performance measures evaluated based on daily flows at the monitoring stations for calibration and validation periods
Table 4.
The Water level efficiency evaluation of EFDC model for calibration and validation periods
| Site |
Calibration (2015 - 2018) |
Validation (2011 - 2014) | ||||
|
mean OBS |
mean SIM | % Diff |
mean OBS |
mean SIM | % Diff | |
| Paldangdam | 25.13 | 25.12 | 0.26 | 25.16 | 25.16 | 0.26 |
3.1.2 수질
HSPF 모형의 수질 보정을 위해 수온, DO를 보정한 후 BOD, TOC, T-N, T-P, Chl-a에 대하여 선행연구를 참고하여 보정을 수행하였으며 (Lee 2013), 본 연구에서는 Gamma Test 조합을 위해 고려한 BOD, TOC, T-P, Chl-a 항목만을 제시하였다. Table 5에서 제시한 바와 같이 보정과 검증 결과 모두 % difference 값이 대부분 15 이하로 산정되어 “Very Good”으로 평가되었다. 모의값과 실측값이 같으면 0에 가까운 값을 나타내는 RMSE의 경우 0.02 - 35.23의 범위로 산정되었다. Table 6은 팔당댐으로 유입되는 주요 하천인 남한강에 대한 HSPF 보정 및 검증 결과를 그림과 함께 추가로 제시한 것이며 모의치가 관측치의 경향을 잘 반영하고 있는 것을 확인할 수 있다. EFDC 모형은 팔당댐2지점을 대상으로 BOD, TOC, T-P, Chl-a의 수질항목을 보정 및 검증을 수행한 결과, % difference값은 모두 15 이하로 산정되어 “Very Good”으로 평가되었으며, RMSE는 0.01 - 6.64의 범위로 산정되었다. 이에 대한 그림은 Table 7에 수질항목별로 도식화하여 제시하였다.
HSPF와 EFDC 모의 결과 모두 복잡한 수질 메커니즘과 유역의 공간적인 특성을 고려할 때 전반적으로 적절히 모의된 것으로 판단된다.
Table 5.
The Water quality calibration and validation results of HSPF and EFDC models
Table 6.
The calibration and Validation Results of HSPF model in Hangang-D (NamHangang)
| Calibration results (2015 - 2018) | Validation results (2011 - 2014) | |
| BOD | 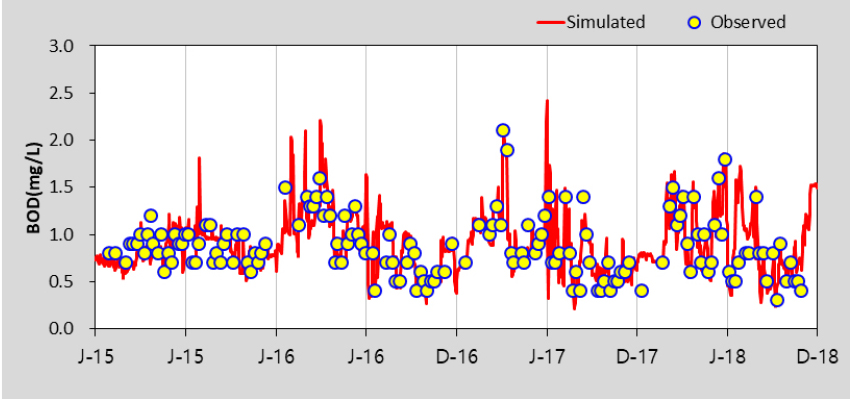 | 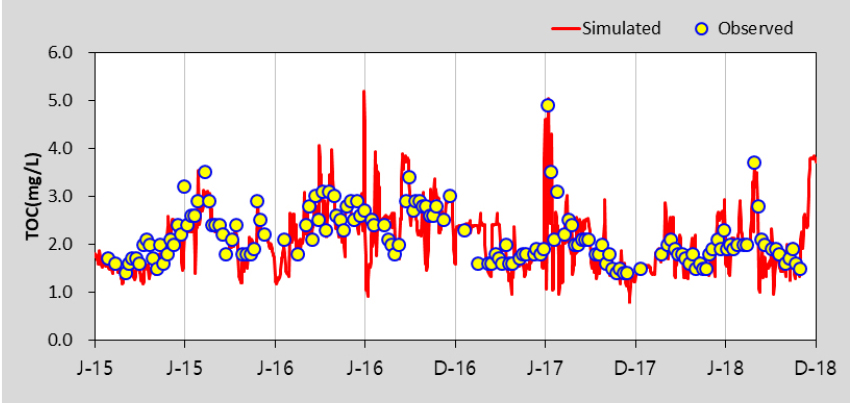 |
| TOC | 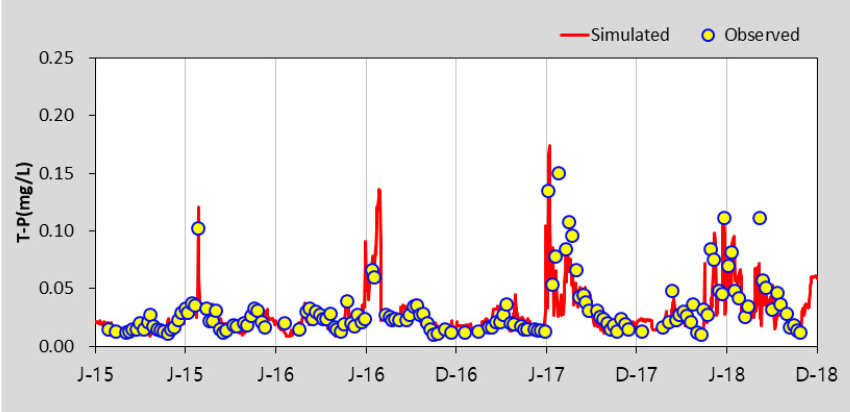 |  |
| T-P |  | 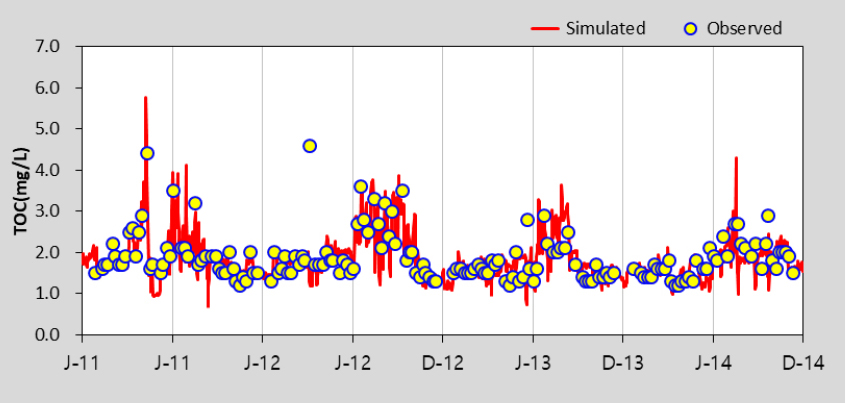 |
| Chl-a | 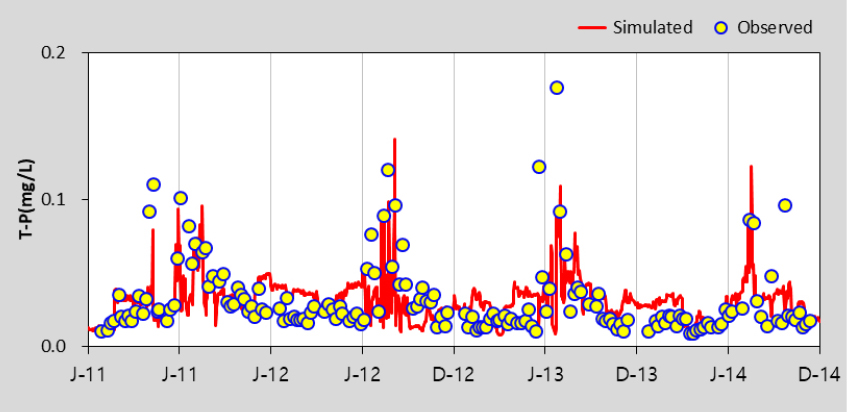 | 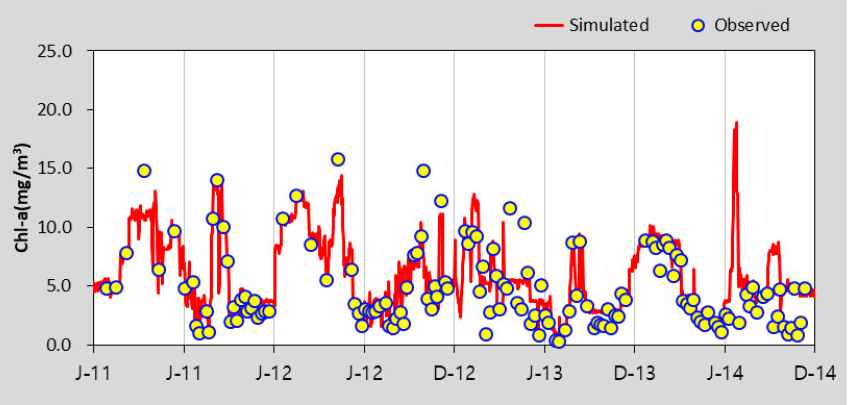 |
Table 7.
The calibration and Validation Results of EFDC model in Paldang Dam – 2
| Calibration results (2015 - 2018) | Validation results (2011 - 2014) | |
| BOD | 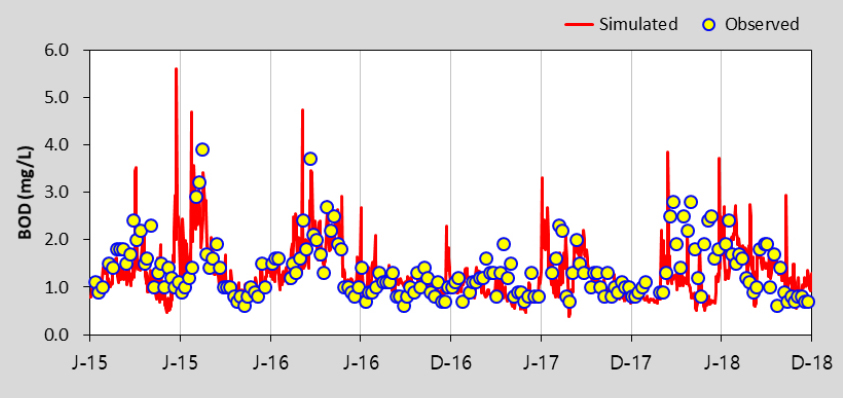 | 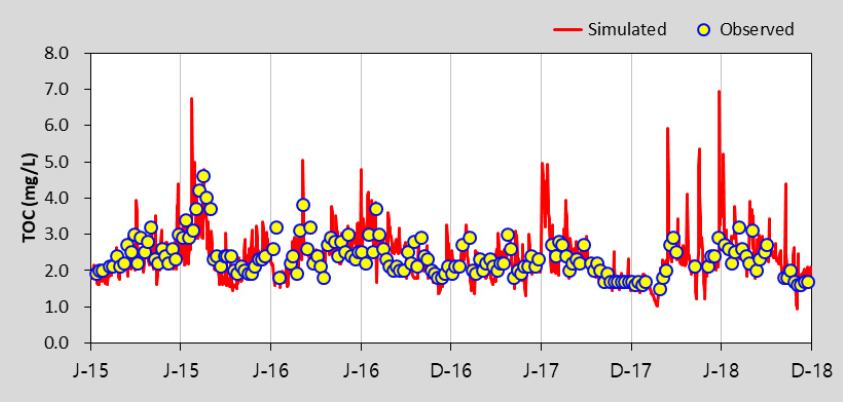 |
| TOC | 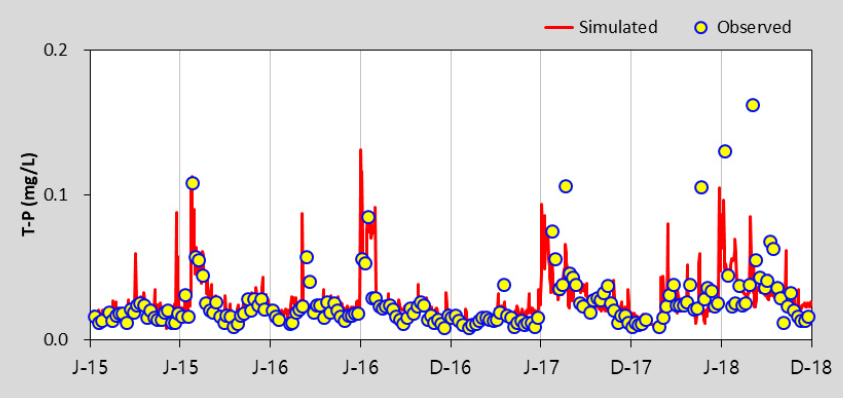 |  |
| T-P | 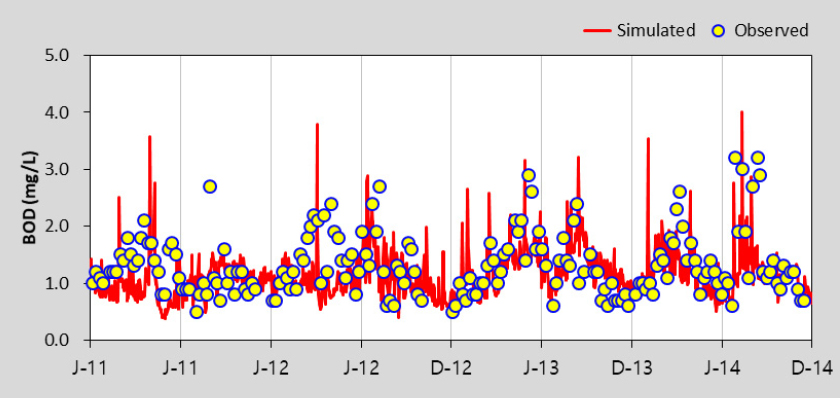 | 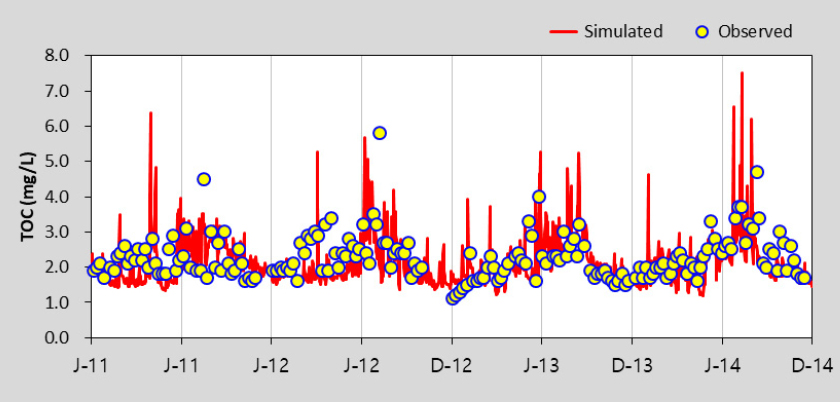 |
| Chl-a | 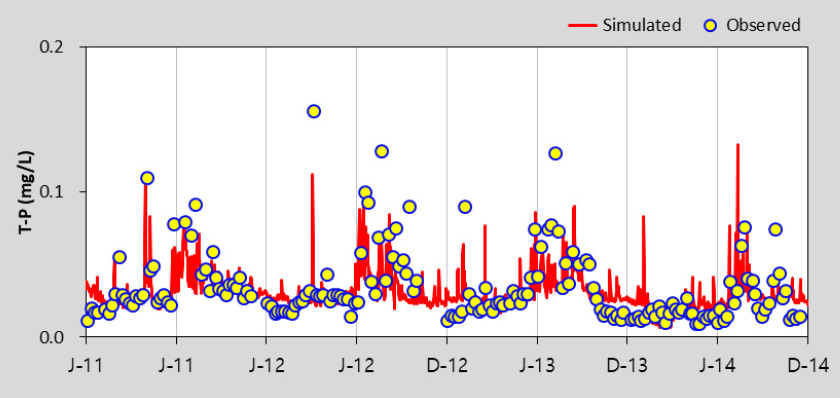 | 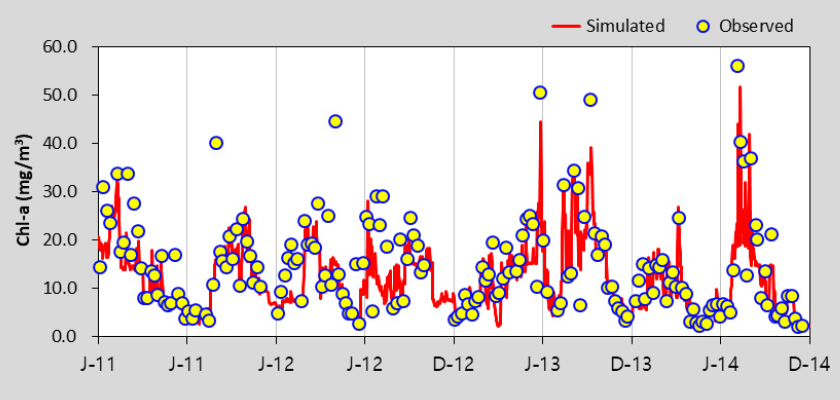 |
3.2 데이터 기반 수질 예측 모형 구성을 위한 불확실성 분석
3.2.1 Gamma Test 적용
데이터 기반의 모형을 이용한 수질예측에 있어 중요한 사항은 유입하천별 다양한 오염원 및 유량조건에 따른 수질특성과 시간적 분포에 따른 입력자료의 조합을 어떻게 구성할 것이지 그리고 어느 정도의 자료를 사용할 것인지 결정하는 것이다. 즉, 예측하고자 하는 대상지점의 수질과 가장 상관성이 있는 유입하천별 수질항목의 자료 조합을 어떻게 구성하는 것이 데이터 기반 모형의 구성에 있어 모의시간을 줄이고 보다 신뢰도 있는 결과를 제시할 수 있는지에 대하여 검토하였다. 먼저 팔당댐 수질을 예측하기 위한 미지의 데이터 기반 모형을 구축하고자 입력 및 출력자료로 앞 절에서 보정 및 검증과정을 거친 물리적 기반 모형으로부터 일단위 수질을 생산하였다. 즉, 하천별 HSPF 모의 수질과 같은 일자의 EFDC 모의 수질을 Gamma Test에 적용하여 최적의 입력자료를 선정하고자 계획하였다.
수질 예측을 목적으로 하는 경우 수질예보와 같이 특정항목에 대한 예·경보발령 등 비상시를 모의하고, 단기적인 예측으로 각종 수질사고에 대비하기 위한 것으로 안정성, 신속성이 중요시된다 (Seo and Choi 2007). 하지만 EFDC 모형의 경우 안정화 기간이 오래 소요되고 모형의 시작시간 역시 초기조건에 영향을 미쳐 모델링 기간에 대한 고찰이 필요하며, 본 연구대상지역을 1년간 모의하는데 약 3시간 소요되는 등 구동시간이 오래 걸리는 단점이 있다 (Oh 2016). 이에 따라 해당 유역의 복잡성과 정밀성을 포함한 과거 수질자료를 기반으로 보다 안정되고 신속하게 표출할 수 데이터 기반 모형 구축을 위한 선행 연구단계의 결과를 제시하였다.
Fig. 4는 Gamma Test를 적용한 흐름도를 제시한 것으로 입력값에 대한 목표값의 정확도를 측정하기 위해서 Gamma Test의 Near Neighbours는 10개의 값을 사용하였다. Gamma Test를 수행 후에 계산되는 결과는 Gamma, Gradient, Standard error, V-ratio로 Gamma의 경우 값이 클수록 자료간의 상관성이 낮고 불확실도가 높음을 나타내고 Standard error는 자료의 표준편차를 나타낸다. Gradient의 경우 값이 급하게 나올수록 수질항목간 관계의 복잡함을 나타내며, V-ratio는 0값에 가까울수록 입력자료를 통한 수질의 예측력이 높음을 나타낸다 (Niknia et al. 2014).
3.2.2 Gamma Test의 결과 해석
본 연구의 수질예측 목표지점은 남한강을 비롯한 총 9개의 하천이 유입되어 영향을 미치는 지점으로 수질항목별 자료가 방대하여 예측하고자 하는 팔당댐2지점의 수질항목과 유입하천별 수질 (BOD, TOC, T-P, Chl-a 등)에 대한 상관성 분석을 수행하였다. 즉, 유입되는 모든 하천을 고려했을 경우와 유입 하천을 하나씩 소거하였을 때의 Gamma, V-ratio값을 비교함으로써 상관성은 더 높고, 자료의 양은 더 적게 입력자료 조합을 구성하는 것을 목표로 하였다. Table 8을 보면 BOD의 경우 모든 하천을 고려했을 경우의 Gamma값은 0.008163이며, 섬강, 흑천, 청미천, 북한강의 제외한 경우의 Gamma값을 보면 0.008163 보다 더 큰 값으로 산정되었는데 이는 모든 하천을 고려했을 때보다 4개 하천의 BOD를 제외하면 상관성이 더 낮아지고 불확실도가 높음을 의미한다. V-ratio값 또한 섬강, 흑천, 청미천, 북한강의 4개 하천을 제외했을 때 값을 보면 모든 하천을 고려했을 때의 0.032652 보다 더 크게 산정되었다. V-ratio값은 0에 가까울수록 입력자료를 통한 수질의 예측력이 높기 때문에 4개의 하천을 입력자료로 포함시켜야 함을 확인할 수 있다. 이에 따라 팔당댐 2지점의 BOD 수질에 가장 큰 영향을 끼치는 하천은 섬강, 흑천, 청미천, 북한강이라고 해석할 수 있다. 이와 같은 방법으로 타 수질항목의 상관성을 분석한 결과 팔당댐 2지점의 TOC는 양화천과 복하천을 제외한 7개의 하천 (남한강, 섬강, 청미천, 흑천, 경안천, 북한강, 조종천 등)에 대한 상관성이 큰 것으로 분석되었다 (Table 9). T-P는 흑천, 경안천, 북한강의 3개의 하천이 Chl-a는 남한강, 청미천, 북한강, 조종천 등 4개의 하천에 대한 영향이 팔당댐2지점의 수질에 영향이 큰 것으로 나타났다 (Tables 10 and 11).수질항목별 Gamma Test 결과를 보면 4개 수질항목 모두 북한강의 영향이 지배적임을 확인할 수 있다. 이는 팔당댐 2지점과의 수직거리가 짧고 인근의 위치한 경안천 유입 유량과 비교했을 경우 유량 규모가 더 크기 때문에 이에 대한 영향으로 판단된다.
Table 8.
The gamma test results to derive the input variable combination for BOD
Table 9.
The gamma test results to derive the input variable combination for TOC
Table 10.
The gamma test results to derive the input variable combination for T-P
Table 11.
The gamma test results to derive the input variable combination for Chl-a
4. 결 론
본 연구에서는 다양한 수문조건에 따른 해당 유역의 복잡성과 정밀성이 재현된 과거와 현재의 일단위 수질을 최대한 확보하고자 물리적 기반 모형을 활용하였으며 이를 기반으로 신속하고 안정된 데이터 기반 모형을 구축하기에 앞서 Gamma Test 기법을 적용하여 최적의 입력자료 조합을 선정하였다.
팔당댐 2지점의 효율적인 수질 예측을 위해 BOD는 섬강, 흑천, 청미천, 북한강의 영향이 가장 크게 나타났고, TOC는 남한강, 섬강, 청미천, 흑천, 경안천, 조종천, 북한강에서 유입되는 영향이 민감한 것으로 분석되었다. T-P의 경우 흑천, 경안천, 북한강, Chl-a는 남한강, 청미천, 조종천, 북한강의 영향이 분석되었다.
본 연구의 결과는 유입하천별 시계열 형태의 수질자료에 대한 불확실성 및 민감도를 사전에 검토하여 반복적인 모의 수행을 지양하고 신뢰도 있는 데이터 기반의 예측 모형을 구축하기 위한 일련의 과정이라고 할 수 있다. 본 연구에서 Gamma Test를 통해 도출한 수질항목별 입력자료 조합으로 데이터 기반 모형을 구축한다면 유입하천별 수질만 있으면 EFDC 모형을 구동하지 않고도 팔당댐 호소 수질의 예측이 가능할 것으로 판단된다.
현재 모델링 관련 연구의 추세는 서로 다른 유형의 모형을 결합하여 최적의 방식을 도출하는 것이다. 이러한 시점에서 본 연구에서 제시한 결과를 토대로 데이터 기반 모형을 구축할 것이며, 이는 물재해 안전성을 강화하는 사전관리 중심의 수질예측 기술을 한 단계 높은 수준으로 진화시킴으로써 보다 빠르고 신뢰도 높은 의사 결정 지원이 가능할 것으로 기대된다.