Analysis of Tree Roughness Evaluation Methods Considering Depth-Dependent Roughness Coefficient Variation

Du Han Lee; Dong Sop Rhee

doi:10.17820/eri.2023.10.3.051

Preview

Original Article

Ecology and Resilient Infrastructure. 30 September 2023. 51-63
https://doi.org/10.17820/eri.2023.10.3.051

Analysis of Tree Roughness Evaluation Methods Considering Depth-Dependent Roughness Coefficient Variation

수심별 조도계수 변화를 고려한 수목 조도공식 특성 분석

Du Han Lee¹

Dong Sop Rhee¹^*

이 두한¹

이 동섭¹^*

¹Research Fellow, Department of Hydro Science and Engineering Research, Korea Institute of Civil Engineering and Building Technology, Goyang-Si 10223, Korea

¹한국건설기술연구원 수자원하천연구본부 연구위원

^{*Corresponding Author}

ABSTRACT

Riverine tree management is crucial in realizing a balance between flood control and ecological preservation, which requires an accurate assessment of the impact of trees on river water elevations. In this study, eight different formulas for evaluating vegetation roughness considering the drag force acting on trees, were reviewed, and the characteristics and applicability of these methods were evaluated from a practical engineering perspective. The study compared the characteristics of vegetation roughness measurement methods for calculated roughness coefficients at different water depths and analyzed factors such as effects of tree canopy width, tree density and diameter, and tree stiffness coefficient, and water level estimation results. A comparison of roughness coefficients at the same water depths revealed that the Kouwen and Fathi-Moghadam formulas and the Fischenich formula yield excessive drag coefficients compared to other formulas. Factors such as channel geometry, tree diameter, and tree density showed varying trends depending on the formula but did not exhibit excessive outliers. Formulas considering the tree stiffness coefficient, such as the Freeman et al.’s formula and the Whittaker et al.’s formula, showed significant variations in drag coefficients depending on the stiffness coefficient. When applied to small- and medium-sized virtual rivers in South Korea using the drag coefficient results from the eight formulas, the results indicated a maximum increase in water level of approximately 0.2 to 0.4 meters. Based on this review, it was concluded that the Baptist et al., Huthoff et al., Cheng, Luhar, and Nepf‘s formulas, which exhibit similar characteristics and low input data uncertainties, are suitable for practical engineering applications.

Keywords

Canopy width

Riverine tree

Tree density

Tree stiffness

Vegetation roughness method

하천내 수목관리는 홍수와 생태 관리의 균형점을 찾는다는 점에서 매우 중요하며 이를 위해서는 수목이 하천 수위에 미치는 영향을 정확하게 평가할 필요가 있다. 본 연구에서 수목에 작용하는 항력을 고려하는 수목조도공식 8개에 대해 검토하여 실무 수리계산의 관점에서 수목 조도계수 공식의 특성과 적용성을 평가하였다. 개별 수목 조도계수 공식의 수심별 조도계수 산정 특성을 비교하고, 수관부 영향, 수목밀도와 직경 영향, 수목 강성계수 영향, 수위 산정 결과 등을 분석하였다. 동일 조건 수심별 조도계수 비교를 통해 Kouwen and Fathi-Moghadam 공식과 Fischenich 공식은 타 공식에 비해 과도한 조도계수를 산정하였다. 수관부, 수목 직경, 수목 밀도 등은 공식에 따라 상이한 경향을 나타내나 과도한 특이점은 없는 것으로 나타났다. 수목 강성계수를 고려하는 Freeman et al. 공식과 Whittaker et al. 공식은 강성계수에 따라 조도계수가 매우 큰 차이를 나타낸다. 8개 공식의 조도계수 산정 결과를 이용하여 국내 중소규모 가상 하천에 적용한 결과 최대 약 0.2 - 0.4 m 정도의 수위 상승 효과를 나타내고 있다. 이상의 검토를 통해 유사한 특성을 가지며 입력자료의 불확실성이 낮은 Baptist et al., Huthoff et al., Cheng, Luhar and Nepf 등의 4개 공식이 실무 적용에 적합한 것으로 판단하였다.

키워드

수관부 폭

하천 수목

수목밀도

수목 조도공식

수목 강성계수

MAIN

1. 서 론
2. 수목 조도공식 검토
2.1 Freeman et al. (2000)
2.2 Kouwen and Fathi-Moghadam (2000)
2.3 Fischenich (2000)
2.4 Baptist et al. (2007)
2.5 Huthoff et al. (2007)
2.6 Cheng (2011)
2.7 Luhar and Nepf (2013)
2.8 Whittaker et al. (2015)
3. 수목 조도 공식 특성 비교
3.1 동일 조건 수심별 조도계수 비교
3.2 수관부의 영향 비교
3.3 수목 밀도와 직경 영향 비교
3.4 수목 강성계수 영향 비교
3.5 가상 하도 적용에 의한 수위 영향 비교
3.6 수리계산 실무 적용성 검토
4. 결 론

1. 서 론

하천 수목은 하천 생태계의 서식처 제공, 하안의 물리적 안정, 오염물 흡착 등의 중요한 기능을 하나, 조도계수 증가와 항력 발생으로 홍수를 악화시키기도 한다. 최근 우리나라에서는 하천 내 수목의 과도한 생장으로 인한 홍수위 상승의 우려가 제기되고 있다. 하천내 수목관리는 홍수와 생태 관리의 균형점을 찾는다는 점에서 매우 중요하며 이를 위해서는 수목이 하천 수위에 미치는 영향을 정확하게 평가할 필요가 있다.

일반적으로 Manning 계수 n으로 표현되는 수목의 조도계수는 0.025 - 0.2 m^-1/3s 사이의 큰 범위를 나타내는데 경우에 따라서는 0.4 m^-1/3s까지 산정되기도 한다. 수목 조도는 수목 자체의 물리적 특성에 따라 변하며 수심과 유속과 같은 수리인자에 따라 변한다. 또한 수목 분포에 큰 영향을 받으며 결과적으로 공간적, 시간적으로 변하게 된다. 수목 조도를 포함하는 하천의 조도 계수 자체도 다양한 인자의 영향을 받으며 공간적, 시간적으로 변하게 되므로 하천 수리 해석에서 적합한 수목 조도를 결정하는 것은 쉽지 않다. Manning 식 (Manning, 1895)을 개발한 Manning 자신도 Manning 조도계수가 수심과 유속에 따라 변하는 계수이므로 사용을 권장하지 않았다 (Freeman, 2000).

현재까지 수목을 포함하는 식생 조도계수를 산정하는 다양한 공식이 제안되었는데 초기에는 초본류에 대한 공식이 제안되었다. 대다수의 공식은 수리해석의 적용성을 위해 Manning 계수 n 또는 Darcy-Weisbach 마찰계수 f로 제시하고 있다. 1940년대에 Palmer (1945)는 식생의 Manning n은 유속 (U)과 동수반경 (R)의 곱에 반비례하는 것을 발견하고 잘 알려지 n-UR 곡선을 제안하였다. Ree (1954)는 야외 실험을 수행하여 다양한 식생에 대한 n-UR 곡선을 제시하였다. Kouwen and Li (1980)는 초본의 생물역학적 특성과 항력에 의한 휨을 고려한 식생 조도 공식을 개발하였다.

일반적으로 수목을 포함하여 흐름에 의한 식생의 항력 는 다음과 같이 표현된다.

(Eq. 1)

F_{d} = \frac{1}{2} C_{d} ρ U^{2} A_{v}

여기서 C _d는 항력계수, ρ는 물의 밀도, U는 식생 부근의 접근 유속, A_v는 흐름방향에 연직면으로 투영된 식생의 전면부 면적 등이다.

Eq. 1에서 A_v를 결정하는 것은 식생의 복잡한 구조, 흐름에 의한 휨과 이로 인한 식생 구조의 변화 등으로 인해 실제로는 매우 어렵다. 현재까지 제안된 수목 조도 공식은 A_v의 계산 방법에 따라 구분할 수 있다. Baptist et al. (2007), Huthoff et al. (2007), Cheng (2011) 등은 식생을 균일하게 분포하는 원통형 강체로 가정하였다. 여기서 잎과 가지에 의한 흐름 저항은 무시하며 줄기에 의한 저항만 고려된다. 이와 같은 방법은 잎과 가지가 거의 없거나 부분 침수된 교목과 관목에 적용될 수 있다. J̈arvel̈a (2004)는 잎이 없는 수목 줄기와 가지의 전면부 면적을 계산하기 위하여 하천 차수 기법 (stream odering scheme)을 도입하였다. Fischenich (2000)와 Whittaker et al. (2015)은 실제로 측정된 A_v를 적용할 것을 제안하였다. J̈arvel̈a (2004)와 Jalonen et al. (2013)는 식생 전면부 면적을 대신하여 원격센싱 자료에서 구한 길이 척도인 잎 면적 색인 (leaf area index, LAI)을 사용하였다. 유연한 식생의 유속에 따른 A_v의 변동을 고려하기 위하여 J̈arvel̈a (2004)와 Whittaker et al. (2015)는 속도에 대한 Vogel 지수 ψ를 항력 공식에 도입하였다. 이에 따라 항력식의 F_d∝ U²관계를 F_d∝ U^2-ψ형태로 제안하였다.

수목 조도에서는 식생의 생물역학적 특성도 고려되는데, Freeman et al. (2000)는 강성 계수 E, Kouwen and Fathi-Moghadam (2000)는 식생 지수 ξE, Whittaker et al. (2015)은 휨강성 EI, Kouwen and Li (1980)는 단위 미터 당 휨강성 MEI 등을 제안하였다. 식생의 휨강성과 LAI 등을 고려하는 공식은 식생을 원통형 강체로 모사하는 방법에 비해 보다 정확할 것으로 기대할 수 있다.

국외에서는 수목 조도 공식을 하천수리해석에 다양하게 적용되고 있다. Gillihan (2013)과 Dombroski and Greimann (2014) 등은 San Joaquin 강의 2차원 수리해석 및 유사해석 (SRH-2D)에서 동적 Manning 계수 산정을 위해 Verschoren et al. (2016)과 Baptist et al. (2007)의 공식을 각각 적용하였다. Abu-Aly et al. (2014)은 SRH-2D 모형에 Casas et al. (2010)의 공식을 추가하고 상이한 흐름 조건에서 식생조도의 공간분포를 예측하기 위하여 LiDAR 데이터에 추출한 식생 높이를 이용하였다.

국내에서는 현재까지도 수목 조도를 Chow (1959)의 조도계수 표에 의해 수심에 대해 고정된 조도계수를 설정하여 계산하는 것이 일반적이다. 다만, Ji et al. (2021)은 지상 LiDAR 측량 결과를 통해 수목 전면부 면적을 추정하고 Baptist (2005)의 공식을 적용하여 2차원 수리해석을 수행한 사례가 있다.

수목 조도 공식을 이용한 연구들은 공통적으로 Chow의 조도계수 표에 의한 고정된 조도계수를 적용하는 것보다 조도계수 공식에서 산정된 Manning n을 적용하는 것이 보다 정확함을 보여준다. 그러나 여전히 수목 조도 공식의 특성과 적용성이 실제 하천 규모에서 충분히 검증되지 못한 실정이다.

본 연구에서는 실무 수리계산적용의 관점에서 수목 조도계수 공식의 특성과 적용성을 평가하고자 한다. 먼저 개별 수목 조도계수 공식의 수심별 조도계수 산정 특성을 비교하고, 수관부 영향, 수목밀도와 직경 영향, 수목 강성계수 영향, 수위 산정 결과 등을 분석하고, 이를 통해 실무적용성을 평가하고자 한다.

2. 수목 조도공식 검토

1차원 또는 2차원 수리계산에 수심평균유속 U은 Manning 공식 또는 Chezy 공식과 같이 동수반경 (R) 또는 수심 (H)과 에너지 경사 (S_f)의 관계로 표현되며 하상 등의 흐름 저항은 Chézy 계수와 Manning 계수로 표현된다. Manning 계수 n과 Chézy 계수 C는 다음과 같다.

(Eq. 2)

n = R^{2 / 3} S_{f}^{1 / 2} / U

(Eq. 3)

C = U / \sqrt{R S}

Eq. 2와 Eq. 3로부터 Chézy 계수와 Manning 계수는 다음과 같은 관계로 표현된다.

(Eq. 4)

C = \frac{1}{n} R^{1 / 6}

수목이 있는 경우의 연직 유속분포는 Fig. 1과 같이 수목 영역 내부에서는 유속이 저하되고 수목 영역 상부에서 유속이 증가하는 구조를 나타낸다. 수목 조도공식은 수목의 영향에 의한 수목 영역 내부의 유속 저하와 수목 영역 상부의 유속분포 변화를 고려하여 조도계수를 계산하는 방법을 제시한다. 현재까지 제안된 수목조도공식은 Eq. 1의 항력 공식과 운동량 보존 법칙으로부터 조도계수 산정식을 유도하는 이론식과 실험결과를 이용한 회귀식 공식으로 나뉜다. 본 연구에서 관련 문헌에서 인용도가 높은 공식 8개에 대해 검토하였으며 대상 공식은 Table 1과 같다. 대상 공식에 대해 자세히 살펴보면 다음과 같다.

https://cdn.apub.kr/journalsite/sites/kseie/2023-010-03/N0190100301/images/kseie_10_03_01_F1.jpg

Fig. 1

Vertical velocity distribution by vegetation effect (Baptist et al. 2007).

Table 1.

Variables and parameters used in vegetation roughness methods

Vegetation roughness method	Physical properties of vegetation					Hydraulic factors
Vegetation roughness method	Plant density	Plant height	Stem diameter	Canopy area	Stiffness	Depth	Velocity	Energy slope
① Freeman et al. (2000)	○	○		○	○	○	○	○
② Kouwen and Fathi-Moghadam (2000)		○			○	○	○
③ Fischenich (2000)	○	○	○	○		○
④ Baptist et al. (2007)	○	○	○			○
⑤ Huthoff et al. (2007)	○	○	○			○
⑥ Cheng (2011)	○	○	○			○
⑦ Luhar and Nepf (2013)	○	○	○	○		○
⑧ Whittaker et al. (2015)	○	○	○	○	○	○	○

2.1 Freeman et al. (2000)

Freeman et al. (2000) 공식은 미공병단에서 주관한 대형 수로 (길이 152.4 m, 높이 1.82 m, 폭 2.44 m)에서 21종의 실제 수목을 이용한 실험을 통해 제안하였다. 실험결과에 의하면 유속이 일정 값 이하에서는 유속이 증가함에 따라 항력이 선형으로 증가하나 일정 유속 이상에서는 유속 증가에 따라 항력이 지수적으로 크게 증가하는 것으로 나타났다.

Freeman은 수목에 의한 흐름 저항은 수목에 의해 발생하는 항력의 총합과 같다고 가정하였다. 수심이 0.8h_p를 초과하면 휨에 의한 영향이 증가하므로 이를 기준으로 공식을 제안하였다. 수목의 휨을 고려하여 항력계수는 Reynolds number, 수심, 수목 높이, 수목 종류, 수목 형태, 수목 휨강성, 수목 밀도 등의 영향을 받는 것으로 가정하였다. 실험결과에 의하면 유속, 수심, 수목 밀도, 수목 휨강성, 수목 간격 등이 증가하면 항력계수는 감소하였다. 실험결과에 의해 수목 항력 및 흐름 저항의 중요 인자는 ① 수목 변형 저항력에 대한 흐름에 의한 항력의 비, ② 수목 높이에 대한 수심비, ③ 하상에서 흐름에 대한 수목 폐색 정도, ④ Reynolds number 등의 4가지 인자로 평가하였으며 이를 기준으로 회귀 분석을 통해 Eq. 5와 같은 수목 조도공식을 제안하였다. 이 식은 수목의 밀도, 높이, 수관폭, 휨 효과 등을 고려할 수 있다.

(Eq. 5)

n = \{\begin{cases} 0.00003487 {(\frac{E_{s} A_{s}}{ρ A_{p}^{*} u_{*}^{2}})}^{0.15} {(m A_{p}^{*})}^{0.166} {(\frac{u_{*} R}{ν})}^{0.622} \\ (\frac{R^{2 / 3} S^{1 / 2}}{u_{*}}), H \leq 0.8 h \\ 0.183 {(\frac{E_{s} A_{s}}{ρ A_{p}^{*} u_{*}^{2}})}^{0.183} {(\frac{h_{p}}{H})}^{0.243} {(m A_{p})}^{0.273} {(\frac{v}{u_{*} R})}^{0.115} (\frac{R^{2 / 3} S^{1 / 2}}{u_{*}}), H > 0.8 h_{p} \end{cases}

여기서 H는 수심, R은 동수반경, u_*는 마찰속도, h_p는 수목 높이, E_s는 수목 강성계수, A_s는 H/4 지점에서 측정된 수목 줄기 단면적, A_p는 수목 전면부 면적, A_p^*는 부분 침수된 수목의 전면부 침수 순면적, m은 수목 밀도, v는 물의 동점성계수 등이다.

2.2 Kouwen and Fathi-Moghadam (2000)

Kouwen and Fathi-Moghadam (2000)은 유속과 침엽수의 Darcy-Weisbach 마찰계수의 상관분석을 통해 Eq. 6과 같이 수목 조도공식을 제안하였다. 이 식은 수목의 높이와 휨 효과를 고려하며 수목 밀도, 직경, 수관폭 등은 고려하지 않는다.

(Eq. 6)

n = 0.228 {(\frac{U}{\sqrt{\frac{ξ E}{ρ}}})}^{- 0.23} {(\frac{H}{h_{p}})}^{0.5}

여기서 ξE는 식생 지수로 2.07 - 4.54 N/m²의 범위를 갖는다.

2.3 Fischenich (2000)

Fischenich (2000)는 운동량 보존식과 항력식에서 정상등류에 대해서 다음과 같은 수목 조도식을 유도하였다. 이 식은 수목의 밀도, 높이, 직경, 수관폭 등을 고려하며 휨 효과는 고려하지 않는다.

(Eq. 7)

n = \frac{R^{^{1 / 6}}}{(\frac{U}{u_{*}}) \sqrt{g})}

(Eq. 8)

\frac{U}{u_{*}} = \begin{matrix} \{\begin{matrix} \sqrt{\frac{2}{C_{d} A_{d} R}}, H \leq h_{p} \\ \frac{2.5}{H} (X + Y), H > 1.1 h_{p} \end{matrix} \end{matrix}

(Eq. 9)

X = 1.26 h_{p}^{2} \frac{2 h_{p}}{11 C_{d} A_{d}} (1 - e^{- 5.5 C_{d} A_{d}})

(Eq. 10)

Y = (H - 0.95 h_{p}) [In (\frac{H}{K h_{p}} - \frac{0.95}{K}) - 1] - 0.05 h_{p} [In (\frac{0.05}{K} - 1)]

(Eq. 11)

K = 0.13 {e^{- (C_{d} A_{d} - 0.4)}}^{2}

여기서 C_d는 항력계수, A_d는 단위 하도길이 당 식생밀도이다.

2.4 Baptist et al. (2007)

Baptist et al. (2007)은 수목을 원통형 강체로 가정하고 Chézy 계수를 적용하여 연직 유속분포를 계산하는 흐름 저항식을 이론적으로 유도하였다. 개발된 이론식을 난류모형을 이용한 정밀한 수치해석 모형의 결과와 비교하여 수정하고 수치해석 모형의 결과와 가장 근사하는 수목 조도 공식을 다음과 같이 제안하였다. 이 식은 수목의 밀도, 높이, 직경 등을 고려하며 휨 효과와 수관폭은 고려하지 않는다.

(Eq. 12)

n = \{\begin{array}{l} H^{1 / 6} \sqrt{\frac{1}{C_{b}^{2}} + \frac{C_{d} m D H}{2 g}}, H \leq h_{p} \\ \frac{H^{1 / 6}}{\sqrt{\frac{1}{1 / C_{b}^{2} + C_{d} m D H / (2 g)}} + \frac{\sqrt{g}}{κ} l n (\frac{H}{h_{p}})} \end{array}, H > h_{p}

여기서 C_b는 하상 Chézy 계수, D는 수목 직경, κ는 von Kármán 상수로 0.40 - 0.41 등이다.

2.5 Huthoff et al. (2007)

Huthoff et al. (2007)은 수목을 원통형 강체로 가정하고 완전 침수 상태에서 수심을 수목에 의한 저항층과 그 상부의 표면층으로 구분하여 각각의 수심평균 유속을 구하고 전체 수심에 의한 수심평균 유속을 구하여 이론적인 수목 조도식을 다음과 같이 제안하였다. 이 식은 수목의 밀도, 높이, 직경 등을 고려하며 휨 효과와 수관폭은 고려하지 않는다.

(Eq. 13)

U = \begin{matrix} \{\begin{matrix} \sqrt{\frac{2 g S_{f}}{C_{d} m D}}, H \leq h_{p} \\ (\sqrt{\frac{h_{p}}{H}} + \frac{H - h_{p}}{H} {(\frac{H - h_{p}}{s})}^{\frac{2}{3} (1 - {(\frac{h_{p}}{H})}^{- 5})}), H > h_{p} \end{matrix} \end{matrix}

(Eq. 14)

s = \sqrt{\frac{1}{m}} - D

(Eq. 15)

n = \frac{H^{2 / 3} \sqrt{S_{f}}}{U}

2.6 Cheng (2011)

Cheng (2011)은 수목을 원통형 강체로 가정하여 운동량 보존식과 항력식에서 다음과 같은 수목 조도식을 유도하였다. 이 식은 수목의 밀도, 높이, 직경 등을 고려하며 휨 효과와 수관폭은 고려하지 않는다.

(Eq. 16)

C = \{\begin{matrix} \sqrt{\frac{π g {(1 - λ)}^{3} D}{2 C_{d} λ H}}, H \leq h_{p} \\ \sqrt{\frac{π g {(1 - λ)}^{3} D}{2 C_{d} λ h_{p}}} {(\frac{h_{p}}{H})}^{3 / 2} + 4.54 \sqrt{g} {(\frac{h_{s}}{D} \frac{1 - λ}{λ})}^{1 / 16} \\ {(\frac{h_{p}}{H})}^{3 / 2}, H > h_{p} \end{matrix}

(Eq. 17)

λ = \frac{m π D^{2}}{4}

(Eq. 18)

n = \frac{H^{1 / 6}}{C}

여기서 λ는 수목 줄기가 있는 하상 면적이며 h_s는 식생이 없는 수면층 두께로 h_s = H-h_p로 계산한다.

2.7 Luhar and Nepf (2013)

Luhar and Nepf (2013)는 수목을 원통형 강체로 가정하여 운동량 보존식과 항력식에서 다음과 같은 수목 조도식을 유도하였다. 이 식은 수목의 밀도, 높이, 직경, 수관폭 등을 고려하며 휨 효과는 고려하지 않는다.

(Eq. 19)

\{\begin{matrix} \sqrt{\frac{π g {(1 - λ)}^{3} D}{2 C_{d} λ H}}, H \leq h_{p} \\ \sqrt{\frac{π g {(1 - λ)}^{3} D}{2 C_{d} λ h_{p}}} {(\frac{h_{p}}{H})}^{3 / 2} + 4.54 \sqrt{g} {(\frac{h_{s}}{D} \frac{1 - λ}{λ})}^{1 / 16} \\ {(\frac{h_{p}}{H})}^{3 / 2}, H > h_{p} \end{matrix}

여기서 C_f는 하상 마찰계수 또는 식생과 수면 사이의 마찰계수이며 A_d단위 하도길이당 수목 밀도 또는 단위 부피 당 수목 전면부 면적을 나타낸다.

2.8 Whittaker et al. (2015)

Whittaker et al. (2015)은 운동량 보존식과 항력식에서 수목의 휨강성을 고려하여 다음과 같은 수목 조도식을 유도하였다. 이 식은 수목의 밀도, 높이, 직경, 수관폭, 휨 효과 등을 모두 고려한다.

(Eq. 20)

n = \sqrt{\frac{C_{d} A_{p}^{*} m C a^{ψ / 5}}{2 g}} H^{1 / 6}

(Eq. 21)

C a = \max (\frac{ρ U^{2} A_{p} h_{p}^{2}}{E I}, 1.0)

여기서 Ca는 식생 코시 넘버 (vegetative Chauchy number)로 수목 휨강성에 대한 항력의 비를 나타내며, ψ는 Vogel 지수로 일반적으로 -0.81을 적용하며, EI는 수목 줄기의 휨강성계수 등이다.

3. 수목 조도 공식 특성 비교

3.1 동일 조건 수심별 조도계수 비교

수목 조도공식별 특성분석을 위해 동일 수목 조건에서의 8개 수목 조도공식의 수심별 조도계수를 계산하여 비교하였다. Freeman et al., Kouwen and Fathi-Moghadam, Luhar and Nepf, Whittaker et al. 등의 공식은 휨강성 등이 필요하므로 수목의 물리적 인자가 알려진 흑버들 (black willow)을 대상으로 Wang and Zhang (2019)의 사례를 참고하여 수목 밀도, 높이, 직경, 휨강성 등을 설정하였다. 이에 따라 수목 밀도 2.3 개/m², 높이 1.22 m, 줄기 직경 0.0189 m, 강성계수 E 1.5E8 N/m², 휨강성계수 EI 0.939 N/m², 수관폭 0.305 m 등으로 설정하였으며, 수리조건은 에너지 경사가 0.001이 되는 조건으로 동일하게 설정하였다. Kouwen and Fathi-Moghadam과 Whittaker et al. 공식은 계산 과정에서 유속에 대한 가정이 필요하여 반복계산을 통해 에너지 경사가 0.001에 수렴하는 조건에서 조도계수를 구하였다. Baptist 공식은 식 내에 하상의 조도를 계산하는 하상 Chézy 계수가 포함되어 있는데, 다른 공식과의 비교를 위해서 하상 Chézy 계수를 충분히 큰 1,000으로 가정하여 하상 조도의 영향을 제거하여 계산하였다. 수심 조건은 6 m까지 설정하여 계산하였으며 수심별 조도계수 계산 결과는 Fig. 2와 같다.

Fig. 2 (a)는 8개 공식의 수심별 조도계수 계산결과를 나타내는데, 동일 조건에서 Kouwen and Fathi-Moghadam 공식이 전체적으로 조도계수를 과대 산정하고 있으며, Fischenich 공식도 타공식에 비해서 수목 높이 이상의 수심에서 조도계수를 과대산정하는 경향을 나타내고 있다. Kouwen and Fathi-Moghadam 공식은 수목 높이인 수심 1.2 m에서 조도계수 0.156을 나타내며 수심 증가에 따라 계속 증가하여 수심 6 m에서는 0.323을 나타낸다. Fischenich 공식은 수심 1.9 m에서 0.116이며 수심 증가에 따라 감소하여 수심 6 m에서는 0.078을 보인다.

Kouwen and Fathi-Moghadam 공식과 Fischenich 공식을 제외하고 나머지 6개 공식에 대해서 자세히 도시하면 Fig. 2 (b)와 같다. 6개 공식은 공통적으로 수목 높이인 1.2 m 부근까지 수심에 따라 조도계수가 급격하게 증가하는 양상을 보이고 있다. Luhar and Nepf 공식은 수심이 수목 높이 이상이 되면 조도계수의 증가 정도는 감소하나 지속적으로 증가하는 추세를 보이며 나머지 5개 공식은 공통적으로 수목 높이 부근의 일정 수심을 정점으로 수심 증가에 따라 조도계수가 완만하게 감소하는 경향을 나타내고 있다.

수심이 수목 높이 1.2 m까지 증가하는 구간에서 Baptist et al., Huthoff et al., Cheng, Luhar and Nepf 등의 공식은 서로 일치하고 있는데, 이는 이들 공식들이 수목의 휨 영향을 고려하지 않는 동일한 가정에서 유도된 이론식이기 때문이다. 그러나 수심이 수목 높이를 초과한 이후에는 수심별 조도계수가 서로 상이한 거동을 나타내며 수심 6 m에서는 공식별 조도계수가 0.031에서 0.069까지의 큰 편차를 나타낸다.

https://cdn.apub.kr/journalsite/sites/kseie/2023-010-03/N0190100301/images/kseie_10_03_01_F2.jpg

Fig. 2

Manning’s n with flow depth for selected methods.

대상 공식 중 유일한 실험 공식인 Freeman et al.의 경우에는 수목 높이 보다 다소 낮은 수심인 1 m에서 최대 조도계수가 나타나며 그 정도는 Whittaker et al.과 유사하게 0.066으로 비교적 높게 산정되며 이후에는 수심 증가에 따라 타 공식에 비해 다소 큰 폭으로 조도계수가 감소하는 경향을 보인다. Baptist et al.은 수목 높이에서 최대 조도계수가 나타나며 그 이후에는 수심 증가에 따라 타공식에 비해 완만하게 조도계수가 감소하는 경향을 보인다. Baptist et al.은 Freeman et al. 공식과 함께 높은 수심에서 조도계수를 낮게 산정하고 있다.

Huthoff et al.은 수심 1.8 m에서 조도계수 0.062의 최대값을 나타내며 이후 수심 증가에 따라 조도계수가 완만하게 감소하는 양상을 나타낸다. 수심 2 m 이상에는 비교 대상 공식 중 중간 정도의 조도계수를 나타내며 수심 6 m에서는 0.044의 값을 보인다. Cheng은 수심 1.9 m에서 조도계수 0.070의 최대값을 나타내며 이후 수심 증가에 따라 조도계수가 완만하게 감소하는 양상을 나타낸다. Cheng은 대상 공식 중 과도한 조도계수를 나타내는 Kouwen and Fathi-Moghadam 공식과 Fischenich 공식을 제외하고 최대 조도계수를 나타내고 있으며 수심이 높은 구간에서는 Luhar and Nepf 공식을 제외하고 가장 높은 값을 나타낸다. Luhar and Nepf 공식은 수심 1.7 m까지 급격하게 증가하나 그 이후이는 완만하게 증가하여 수심 6 m에서는 0.069를 나타낸다.

전체적으로 Kouwen and Fathi-Moghadam, Fischenich, Luhar and Nepf 등의 공식을 제외한 나머지 공식은 상대적으로 유사한 거동을 보이고 있으나 수심별 조도계수의 편차는 최대 0.02 정도로 다소 크게 나타나고 있다.

3.2 수관부의 영향 비교

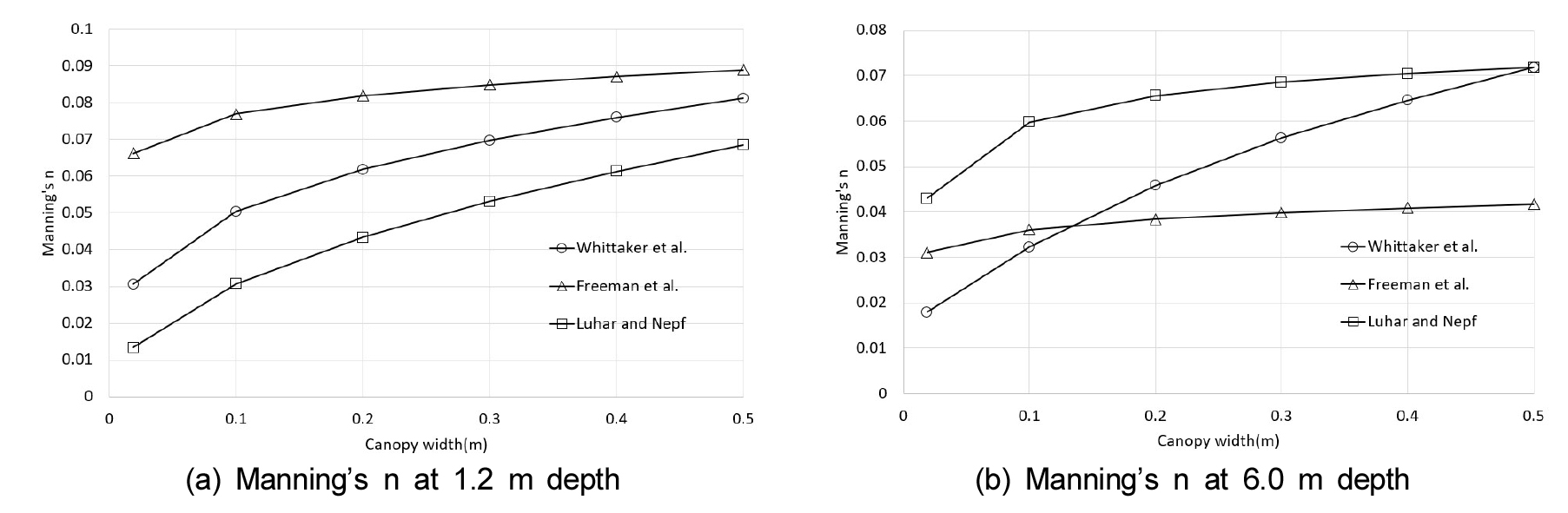
본 연구에서는 수목의 가지와 잎 영역을 수관부로 지칭하였다. 수관부는 나무줄기보다 큰 전면부 면적을 가지므로 항력에 의한 흐름 저항으로 수목 조도계수에 큰 영향을 미친다. 검토 대상 공식 중 수관부의 영향을 고려하는 공식은 Freeman et al., Fischenich, Luhar and Nepf, Whittaker et al. 등 4개인데 이 중 Fischenich 공식은 타공식과 편차가 심하여 제외하고 나머지 3개 공식에 대해 수관부의 영향을 검토하였다. 수관부 폭에 따른 조도계수 계산결과는 Fig. 3과 같다.

https://cdn.apub.kr/journalsite/sites/kseie/2023-010-03/N0190100301/images/kseie_10_03_01_F3.jpg

Fig. 3

Manning’s n with canopy width for selected methods.

여기서 식생 조건은 3.1과 같은 조건으로 설정하고 수관부 폭만 조정하였다. Fig. 3 (a)는 수심이 수목 높이와 유사한 1.2 m인 경우이며 Fig. 4 (b)는 수심 6 m인 경우를 나타내고 있다.

수심 1.2 m에서는 3개 공식이 수관폭 증가에 따라 조도계수가 완만하게 증가하는 양상을 나타내는데, 상대적으로 Freeman et al.은 조도계수를 높게 산정하나 수관폭 증가에 따른 조도계수 증가는 둔감한 것으로 나타난다. 수심 6 m의 경우에는 수관폭 증가에 따라 조도계수가 증가하나 증가폭이 상이하게 나타난다. Luhar and Nepf 공식는 상대적으로 높은 조도계수를 나타내며 완만하게 증가하는 양상을 보이나, Whittaker et al. 공식은 수관폭이 작은 경우에는 조도계수를 낮게 산정하나 수관폭 증가에 따라 조도계수가 급격하게 상승한다. Freeman et al.의 경우에는 수관폭 증가에 따라 조도계수 증가가 매우 완만하게 나타난다. 전체적으로 수관부를 고려하는 공식들 간의 과도하게 특이한 특성은 없는 것으로 판단된다.

https://cdn.apub.kr/journalsite/sites/kseie/2023-010-03/N0190100301/images/kseie_10_03_01_F4.jpg

Fig. 4

Manning’s n with tree density and diameter for selected methods.

3.3 수목 밀도와 직경 영향 비교

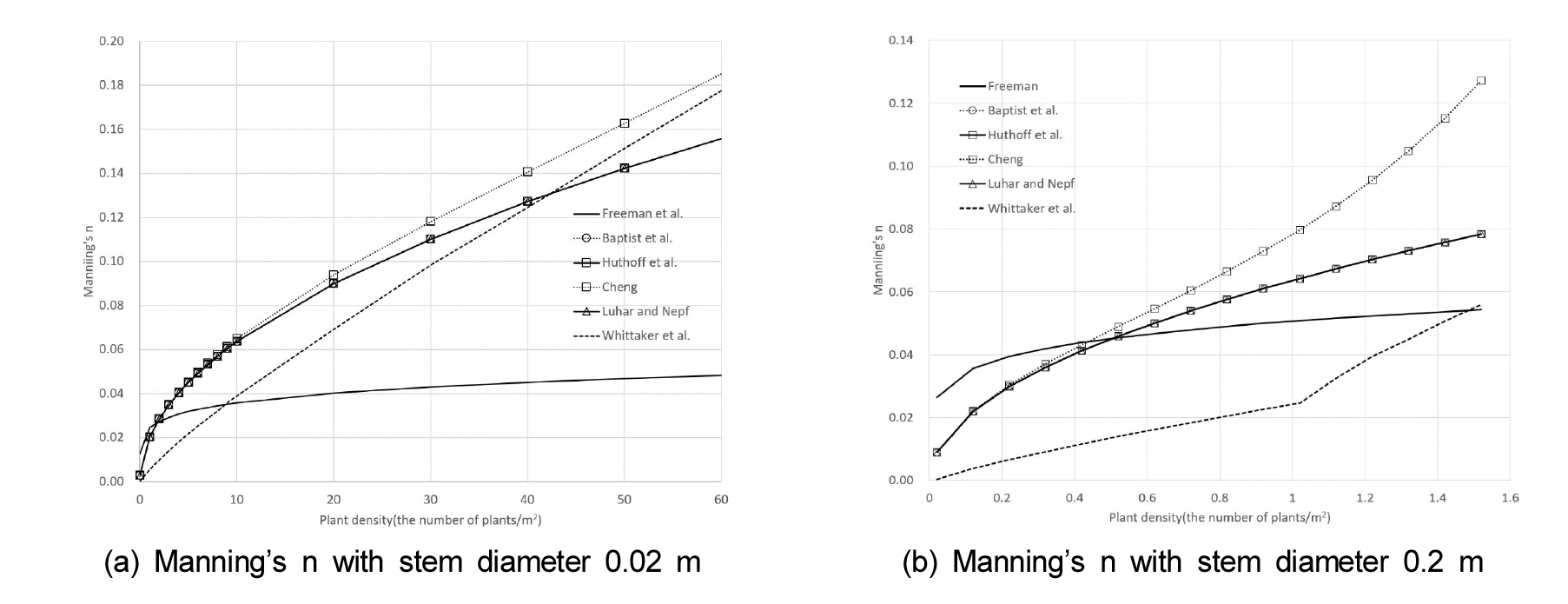
수목 조도계수에서 중요한 요소 중의 하나인 수목 밀도와 직경의 영향을 비교하였다. 수목 밀도와 직경이 증가하면 흐름 저항이 증가하므로 수목 조도계수는 당연히 증가하나, 실제 수목 분포는 직경이 큰 경우에는 밀도가 낮게 나타난다. 본 연구에서는 실제와 유사한 수목 밀도와 직경 조건에서 공식별 조도계수 산정 특성을 비교하였다. 하천 수목에 대한 밀도와 직경 관련 자료가 부재하여 수목 면적과 산정 조도계수를 고려하여 적정한 범위를 설정하였다. 대상 공식은 조도계수를 과대산정하는 Kouwen and Fathi-Moghadam과 Fischenich 공식을 제외한 6개 공식이며 수심은 0.5 m인 경우이며 수목밀도를 제외한 나머지 조건은 3.1과 동일하게 설정하였다. 동일 수목 직경에 수목 밀도를 변화시키며 조도계수의 변화를 비교하였으며 결과는 Fig. 4와 같다.

Fig. 4 (a)는 수목 직경이 0.02 m인 경우 수목 밀도 최대 60개/m²까지 수목 밀도에 따른 공식별 조도계수 산정 결과를 보여준다. Fig. 2와 유사하게 Baptist et al., Huthoff et al., Cheng, Luhar and Nepf 등 3개 공식은 거의 유산한 결과를 나타내며, Freeman et al.은 전체적으로 조도계수가 낮게 나타나며 수목밀도 증가에 따른 조도계수의 상승이 작게 나타난다. Whittaker et al.은 수목 밀도 증가에 따라 거의 선형적으로 조도계수가 증가하는 양상을 보이며, 나머지 공식들은 수목밀도 증가에 따라 초반에는 급격한 조도계수 증가가 나타나지만 이후에는 다소 완만해지는 경향을 보인다. 전체적으로 Freeman et al.을 제외하면 조도계수의 증가폭은 매우 크게 나타난다.

Fig. 4 (b)는 수목 직경이 0.2 m인 경우 수목 밀도 증가에 따른 공식별 조도계수 산정 결과를 보여준다. Fig. 4 (a)와는 수목 직경 외의 다른 조건은 동일함에도 공식별 조도계수 특성을 다소 상이한 양상을 보인다. Baptist et al., Huthoff et al., Cheng, Luhar and Nepf 등 3개 공식은 수목 직경 0.02 m인 경우와 유사한 경향을 나타내고 있고 Freeman 공식도 유사한 경향을 보이고 있으나, Whittaker 공식은 상대적으로 조도계수가 낮게 나타나고 있으며, Cheng 공식은 밀도 증가에 따라 조도계수가 급격하게 증가하는 양상을 보인다.

3.4 수목 강성계수 영향 비교

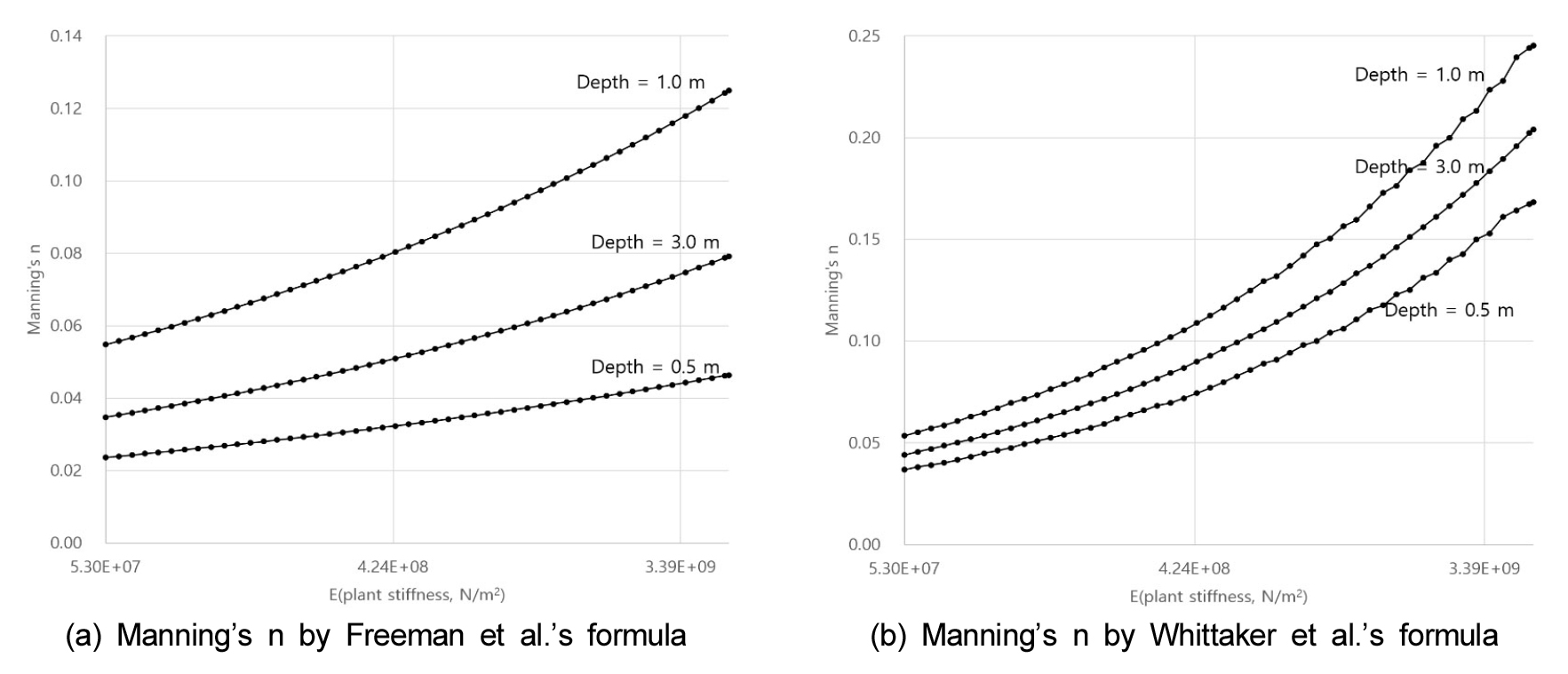
대상 공식 중 Freeman et al., Kouwen and Fathi-Moghadam, Whittaker et al. 등의 3개 공식은 수목의 휨영향을 고려하고 있는데, 이 중 Kouwen and Fathi-Moghadam은 3.1에서 검토한 것과 같이 타 공식에 비해 편차가 크므로 제외하고, 나머지 두 개 공식에 대해 휨 영향을 검토하였다. 수목 강성계수는 실측 (Freeman et al. 2000)에 의하면 5.3E7-4.8E9 N/m²의 값을 보이므로 이 범위에 대해 3.1과 같은 조건에서 수목 강성계수의 영향을 수심별로 계산하면 Fig. 5와 같다.

두 공식 모두 강성계수의 변화에 따라 조도계수가 큰 영향을 받는데, 최대 조도계수가 발생하는 수심 1 m에서 Freeman et al.의 경우 0.055 - 0.125의 조도계수를 나타내며, Whittaker et al.의 경우 0.053 - 0.245를 나타낸다. 강성계수의 증가에 따라 조도계수가 증가하는 정도는 Whittaker et al.이 더 크다. 이 두 공식을 적용하기 위해서는 강성계수에 대한 정확한 설정이 중요함을 알 수 있다.

https://cdn.apub.kr/journalsite/sites/kseie/2023-010-03/N0190100301/images/kseie_10_03_01_F5.jpg

Fig. 5

Manning’s n with tree stiffness for selected methods.

3.5 가상 하도 적용에 의한 수위 영향 비교

8개 수목조도계수 공식의 적용에 따른 수위 영향을 비교하기 위하여 가상의 중소하천에 적용하였다. 수로 규모는 하폭 80 m, 양안 고수부지 폭 20 m, 저수로 폭 35 m, 저수로 깊이 2 m 등으로 가정하였고, 마찰경사는 0.001로 가정하였으며, 우안 중간 1 km 구간의 고수부지에 3.1과 동일한 조건의 수목이 존치하는 것으로 가정하였다 (Fig. 6). 최대 유량은 706 m³/s으로 가정하여 유사한 규모 하천의 실제 홍수량 유입곡선을 이용하여 수문곡선 (Fig. 7)을 생성하여 상류경계조건으로 적용하였다. 하류경계조건은 수위를 등류수심조건으로 가정하였으며 HEC-RAS 모형을 이용하여 부정류 해석을 수행하였다. 수목이 없는 하상과 고수부지의 조도계수는 0.03으로 가정하였고 수위 상승 효과는 수목 구간의 조도계수를 0.03으로 가정하여 비교하였다. 산정된 수목조도계수는 하상 조도계수 0.03을 고려하여 합성 조도계수를 산정하였다 (Table 2). 산정된 조도계수는 HEC-RAS 모형의 가변수심 조도계수 설정에 따라 표 형태로 입력하였다.

https://cdn.apub.kr/journalsite/sites/kseie/2023-010-03/N0190100301/images/kseie_10_03_01_F6.jpg

Fig. 6

Schematic diagram of the test channel.

https://cdn.apub.kr/journalsite/sites/kseie/2023-010-03/N0190100301/images/kseie_10_03_01_F7.jpg

Fig. 7

Inflow hydrograph at No. 25.

Table 2.

Manning n for the test channel

Methods	Max. Manning’s n		Manning n at 6 m depth
Methods	Depth (m)	Manning n	Manning n at 6 m depth
① Freeman et al. (2000)	1.0	0.073	0.043
② Kouwen and Fathi-Moghadam (2000)	6.0	0.324	0.084
③ Fischenich (2000)	1.9	0.120	0.324
④ Baptist et al. (2007)	1.2	0.061	0.045
⑤ Huthoff et al. (2007)	1.8	0.069	0.054
⑥ Cheng (2011)	1.9	0.076	0.063
⑦ Luhar and Nepf (2013)	6.0	0.075	0.075
⑧ Whittaker et al. (2015)	1.1	0.073	0.059

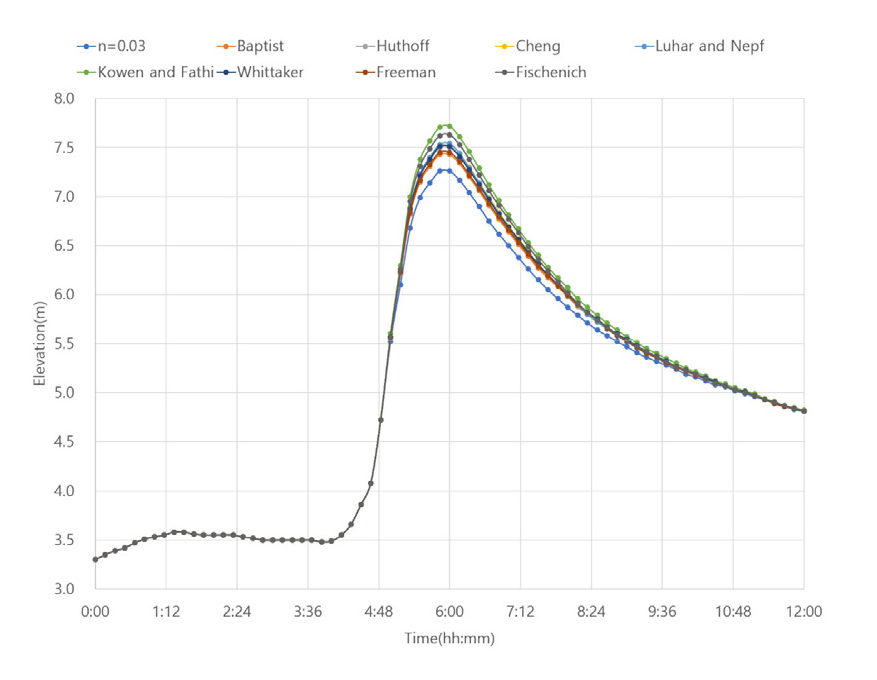
계산 결과 No. 15 지점에서 최대 수위 상승이 발생하며 이 지점의 공식별 수위를 계산 시간에 따라 나타내면 Fig. 8과 같으며 공식별 최대 수위와 수위 차이를 나타내면 Table 3과 같다. Kouwen and Fathi-Moghadam과 Fischenich 공식은 각각 0.45 m, 0.36 m의 높은 수위 상승을 나타내고 있으며 나머지 공식은 0.17 m - 0.27 m의 수위 상승을 나타내고 있다. Huthoff et al., Cheng, Luhar and Nepf, Whittaker et al. 등의 공식은 0.24 m - 0.27 m로 서로 유사한 수위 상승을 나타내고 있다.

https://cdn.apub.kr/journalsite/sites/kseie/2023-010-03/N0190100301/images/kseie_10_03_01_F8.jpg

Fig. 8

Water surface elevations of the test channel at No. 15.

Table 3.

Comparison of water elevation differences for the test channel

Methods	Max. water elevation (m)	Water elevation difference (m)
① Freeman et al. (2000)	7.45	+0.19
② Kouwen and Fathi-Moghadam (2000)	7.71	+0.45
③ Fischenich (2000)	7.62	+0.36
④ Baptist et al. (2007)	7.43	+0.17
⑤ Huthoff et al. (2007)	7.50	+0.24
⑥ Cheng (2011)	7.53	+0.27
⑦ Luhar and Nepf (2013)	7.53	+0.27
⑧ Whittaker et al. (2015)	7.51	+0.25
n = 0.03	7.26	-

3.6 수리계산 실무 적용성 검토

본 연구에서는 8개의 수목 조도공식을 수심별 조도계수 산정 결과, 수관부 영향, 수목밀도와 직경 영향, 수목 강성계수 영향, 수위 산정 결과 등을 통해 비교하였다. 본 연구의 목적은 수리계산 실무 적용에 적합한 공식을 선정하는 것이므로 이에 따라 적합한 공식을 검토하고자 한다.

수목 조도공식의 한계는 각 조건에서 수목 조도의 참값을 알 수 없다는 점이다. 각 공식의 합리적인 유도과정을 통해 실험 자료를 통해 검증되었으나 실제 하천 규모에서의 수목 조도의 참값을 알기 어려우므로 여전히 한계를 가진다. 본 연구에서 검토한 것과 같이 동일한 조건에서도 공식별 편차가 매우 크게 나타나고 있다. 각 공식의 정확도를 참값을 기준으로 평가하는 것은 한계가 있으므로 본 연구에서는 상대적인 비교를 통해 과도하게 특이한 특성을 나타내는 공식은 제외하는 것이 합리적이라고 판단하였다.

우선 동일 조건 수심별 조도계수 비교 (Fig. 2 (a))에 의하면 Kouwen and Fathi-Moghadam 공식과 Fischenich 공식은 수심이 수목을 월류한 상태에서 조도계수가 0.1 이상의 높은 값을 나타내고 있다. Chow (1959)의 조도계수 표에 의하면 조도계수 0.1 이상은 줄기 직경이 큰 버드나무가 밀생한 상태를 나타낸다. 또한 다양한 수목 조건을 실험한 Freeman et al. (2000)에 의하면 줄기 직경 0.02 m에 수목 밀도 4 개/m²의 조건에서 수심이 수목 높이 부근이 경우에 조도계수가 0.07 또는 0.08로 산정된다. 본 연구의 비교 조건인 줄기 직경 0.0189 m과 수목 밀도 2.3 개/m²를 고려하면 Kouwen and Fathi-Moghadam 공식과 Fischenich 공식의 산정결과는 Chow 조도계수 표와 수목 실험 결과와의 편차가 큰 편이므로 실무적인 적용에는 적합하지 않은 것으로 판단된다.

수관부 영향은 3개 공식만 비교하였고 그 영향이 공식마다 상이하기나 하나 과도하게 특이한 특성을 보이는 공식은 없는 것으로 판단된다. 수목밀도와 직경 영향 비교에서는 Freeman et al.은 수목 직경이 낮은 경우 상대적으로 낮은 조도계수를 산정하고 Whittaker et al.은 수목 직경이 중간 정도인 경우 상대적으로 낮은 조도계수를 산정하나 나머지 공식들은 유사한 특성을 보이는 것으로 판단된다. 수목 강성계수 비교에서는 수목 강성계수를 고려하는 Freeman et al. 공식과 Whittaker et al. 공식은 강성계수에 따라 조도계수가 매우 큰 차이를 나타내고 있다. 즉, 강성계수가 부정확할 경우 조도계수 결과의 부정확성이 높아지는데, 국내 수목의 강성계수를 대부분 추정하여야 하므로 계산의 부정확도가 높을 것으로 예상된다. 그러므로 이 2개 공식은 실무적 적용에 적합하지 않은 것으로 판단된다.

이상과 같이 4개 공식을 제외하면 Baptist et al., Huthoff et al., Cheng, Luhar and Nepf 등 4개 공식이 유사한 특성을 보이는 공식으로 실무 적용에 적합할 것으로 판단된다.

4. 결 론

수목 조도공식은 수목 항력 평가를 통해 조도계수를 평가하고 있으나 수목 흐름이 가지는 복잡한 과정을 단순화하는 과정에서 공식별로 다양한 편차가 발생한다. 본 연구에서는 문헌 검토를 통해 국외의 대표적인 수목 조도계수 공식 8개를 선정하여 실무적용 관점에서 공식별 특성을 검토하였다.

동일 조건 수심별 조도계수 비교를 통해 각 공식의 조도계수 특성을 비교하였는데 Kouwen and Fathi-Moghadam 공식과 Fischenich 공식은 타 공식에 비해 과도한 조도계수를 산정하였다. Freeman et al., Fischenich, Luhar and Nepf, Whittaker et al. 등 3개 공식은 수관부를 고려하는 공식으로 그 특성을 비교한 결과 다소 다른 양상을 나타내나 과도한 특이점은 없는 것으로 판단되었다. 수목밀도와 직경 영향 비교에서는 Freeman et al.은 수목 직경이 낮은 경우 상대적으로 낮은 조도계수를 산정하고 Whittaker et al.은 수목 직경이 중간 정도인 경우 상대적으로 낮은 조도계수를 산정하나 나머지 공식들은 유사한 특성을 보이는 것으로 판단되었다. 수목 강성계수 비교에서는 수목 강성계수를 고려하는 Freeman et al. 공식과 Whittaker et al. 공식은 강성계수에 따라 조도계수가 매우 큰 차이를 나타내고 있다. 수목 강성계수는 수종과 직경에 따라 편차가 크나, 현장 계측이 어렵고 국내에서는 계측 사례가 거의 없어 자료의 불확실성이 높다. 8개 공식의 조도계수 산정 결과를 이용하여 국내 중소규모 가상 하천에 적용한 결과 최대 약 0.2 - 0.4 m 정도의 수위 상승 효과를 나타내고 있다. 이상의 검토를 통해 유사한 특성을 가지며 입력자료의 불확실성이 낮은 Baptist et al., Huthoff et al., Cheng, Luhar and Nepf 등의 4개 공식이 실무 적용에 적합한 것으로 판단하였다.

수목조도는 수목과 흐름의 상호작용이 복잡한 구조를 가지며 또한, 수목 자체의 형상과 물리적 특성이 규격화하기 어려워 상당한 불확실이 불가피하다. 공학적인 관점에서 실무 적용은 안정측에서 접근하는 것이 일반적이므로 이와 같은 불확실성을 고려하여 다수의 공식을 비교·검토하여 안정측의 조도계수를 실무적으로 적용하는 것이 타당할 것으로 판단된다.

Acknowledgements

본 연구는 환경부 학술연구용역 ‘하천에서 나무심기 및 공작물 설치 등 관리개선방안연구’의 일환으로 수행되었음.

References

Abu-Aly, T., Pasternack, G., Wyrick, J., Barker, R., Massa, D., and Johnson, T. 2014. Effects of LiDAR-derived, spatially distributed vegetation roughness on two-dimensional hydraulics in a gravel-cobble river at flows of 0.2 to 20 times bankfull. Geomorphology 206: 468-482. 10.1016/j.geomorph.2013.10.017

Baptist, M.J. 2005. Modelling floodplain biogeomorphology. PhD thesis, Delft University of Technology, Faculty of Civil Engineering and Geosciences, Section Hydraulic Engineering, Delft.

Baptist, M.J., Babovic, V., Rodríguez, J., Keijzer, M., Uittenbogaard, R., Mynett, A., and Verwey, A., 2007. On inducing equations for vegetation resistance. J. Hydraul. Res. 45(4): 435-450. 10.1080/00221686.2007.9521778

Casas, A., Lane, S.N., Yu, D., and Benito, G., 2010. A method for parameterising roughness and topographic sub-grid scale effects in hydraulic modelling from LiDAR data. Hydrol. Earth Syst. Sci. 14(8): 1567-1579. 10.5194/hess-14-1567-2010

Cheng, N.S. 2011. Representative roughness height of submerged vegetation. Water Resour. Res. 47(8): W08517. 10.1029/2011WR010590

Chow, V.T. 1959. Open channel hydraulics. New York: McGraw-Hill.

Dombroski, D. and Greimann, B.P. 2014. A deterministic spatially distributed ecohydraulic model for lmproved riverine system management. Technical Rep. No. SRH-2014-26. Denver: Bureau of Reclamation, Technical Service Genter, Sedimentation and River Hydraulics Group.

Fischenich, J.C. 2000. Resistance due to Vegetation. ERDC TN-EMRRP-SR-07, U.S. Army Engineer Research and Development Center, Vicksburg, Mississippi.

Freeman, G.E., Rahmeyer, W.J., and Copeland, R.R. 2000. Determination of resistance due to shrubs and woody vegetation. ERDC/CHL TR-00-25. Vicksburg, MS: US Army Corps of Engineers Research and Development Center. 10.21236/ADA383997

Gillihan, T. 2013. Dynamic vegetation roughness in the riparian zone. M.Sc. thesis, Dept. of Civil Engineering, Univ. of New Mexico.

Huthoff, F., Augustijn, D., and Hulscher, S.J. 2007. Analytical solution of the depth-averaged flow velocity in case of submerged rigid cylindrical vegetation. Water Resour. Res. 43(6): W06413. 10.1029/2006WR005625

Jalonen, J., J̈arvel̈a, J., and Aberle, J., 2013. Leaf area index as vegetation density measure for hydraulic analyses. J. Hydraul. Eng. 139(5): 461-469. 10.1061/(ASCE)HY.1943-7900.0000700

J̈arvel̈a, J. 2004. Determination of flow resistance caused by nonsubmerged woody vegetation. Int. J. River Basin Manage. 2(1):61-70. 10.1080/15715124.2004.9635222

Ji, U., Jang, E., Ahn, M., and Bae, I. 2021. Evaluation of Flow Resistance Coefficient based on Physical Properties of Vegetation in Floodplains and Numerical Simulation of the Changes in Flow Characteristics. Ecology and Resilient Infrastructure 8(4): 212-222.

Kouwen, N. and Fathi-Moghadam, M. 2000. Friction factors for coniferous trees along rivers. J. Hydraul. Eng. 126(10): 732-740. 10.1061/(ASCE)0733-9429(2000)126:10(732)

Kouwen, N. and Li, R.M. 1980. Biomechanics of vegetative channel linings. J. Hydraul. Div. 106(6): 1085-1103. 10.1061/JYCEAJ.0005444

Luhar, M. and Nepf, H.M. 2013. From the blade scale to the reach scale: A characterization of aquatic vegetative drag. Adv. Water Resour. 51: 305-316. 10.1016/j.advwatres.2012.02.002

Manning, R., 1895. On the flow of Water in Open Channels and Pipes. Transactions Institute of Civil Engineers of Ireland 20: 161-209.

Palmer, V.J. 1945. A method for designing vegetated waterways. Agric. Eng. 26(12): 516-520.

Ree, W. 1954. Handbook of channel design for soil and water conservation: Soil conservation service. Washington, DC: USDA.

Verschoren, V., Meire, D., Schoelynck, J., Buis, K., Bal, K.D., Troch, P., Meire, P., and Temmerman, S., 2016. Resistance and reconfiguration of natural flexible submerged vegetation in hydrodynamic river modelling. Environ. Fluid Mech. 16(1): 245-265. 10.1007/s10652-015-9432-1

Wang, J. and Zhang, Z. 2019. Evaluating Riparian Vegetation Roughness Computation Methods Integrated within HEC-RAS. Journal of Hydraulic Engineering 145(6). 10.1061/(ASCE)HY.1943-7900.0001597

Whittaker, P., Wilson, C.A., and Aberle, J. 2015. An improved Cauchy number approach for predicting the drag and reconfiguration of flexible vegetation. Adv. Water Resour. 83: 28-35. 10.1016/j.advwatres.2015.05.005

Ecology and Resilient InfrastructureISSN:2288-8527(Online)응용생태공학회

Preview

Analysis of Tree Roughness Evaluation Methods Considering Depth-Dependent Roughness Coefficient Variation

ABSTRACT

MAIN

(Eq. 1)

(Eq. 2)

(Eq. 3)

(Eq. 4)

Fig. 1

Vertical velocity distribution by vegetation effect (Baptist et al. 2007).

Table 1.

Variables and parameters used in vegetation roughness methods

(Eq. 5)

(Eq. 6)

(Eq. 7)

(Eq. 8)

(Eq. 9)

(Eq. 10)

(Eq. 11)

(Eq. 12)

(Eq. 13)

(Eq. 14)

(Eq. 15)

(Eq. 16)

(Eq. 17)

(Eq. 18)

(Eq. 19)

(Eq. 20)

(Eq. 21)

Fig. 2

Manning’s n with flow depth for selected methods.

Fig. 3

Manning’s n with canopy width for selected methods.

Fig. 4

Manning’s n with tree density and diameter for selected methods.

Fig. 5

Manning’s n with tree stiffness for selected methods.

Fig. 6

Schematic diagram of the test channel.

Fig. 7

Inflow hydrograph at No. 25.

Table 2.

Manning n for the test channel

Fig. 8

Water surface elevations of the test channel at No. 15.

Table 3.

Comparison of water elevation differences for the test channel

Acknowledgements

References