1. 서 론
2. 무참조점 표면유속 산정 기법 개발
3. 드론 영상을 활용한 무참조점 표면유속 산정
3.1 연구 장비
3.2 대상지 선정 및 참조점 측량
3.3 표면유속 측정 실험
4. 결 론
1. 서 론
하천의 유량 측정은 수자원 계획 수립 및 하천 방재의 기초 자료 수립을 위해 필요하다. 기존 국내 유량측정기법은 유속계와 부자를 이용한 기법이며 홍수 시에는 안전상의 이유로 부자를 이용한 기법에 의존해왔다. 하지만 유속계를 이용한 유량측정기법은 고가의 장비가 필요하며 인력이 많이 필요하다는 단점이 있고, 부자를 이용한 유량측정기법은 측정자의 주관 및 측정 환경에 따른 오차 때문에 정확도가 높지 않다는 단점이 있다. 이에 대한 대안으로 최근에는 하천 영상을 이용한 표면영상유속계로 하천의 유량을 측정하는 연구가 활발히 진행 중이다.
표면영상유속계를 이용한 유량 측정은 영상을 이용하기 때문에 카메라 외에 고가의 장비나 인력이 필요 없어 경제적이고 안전하며 넓은 범위의 유속을 순간적으로 측정할 수 있다는 장점이 있다. 최근에는 넓은 범위의 하천 영역을 촬영하여 유속 및 유량을 측정하기 위해 항공기나 드론 영상을 이용한 연구도 활발히 진행 중이다. 특히 항공기에 비해 드론은 운용이 쉽고 시간과 공간에 대한 해상도가 높아 하천의 물리량을 측정하는데 적합하다. 또한 하천 구조물 주변이나 보 월류부 등 직접 유속을 측정하거나 카메라로 촬영하기 힘든 곳에서의 영상을 담기 쉽다는 점도 큰 강점이다. 게다가 드론 영상은 내장 소프트웨어와 짐벌이라는 하드웨어를 통해 원근에 대한 영상 왜곡이 작은 영상을 얻을 수 있다. 또한 열화상 카메라 등 드론에 장착 가능한 다양한 센서를 활용하면 야간에도 영상 촬영이 가능해 드론의 하천 유속 측정에 대한 잠재력이 높다고 할 수 있다.
이에 따라 하천의 드론 영상을 활용하여 하천 표면유속을 측정하는 연구도 활발히 진행 중이다. 국외 연구의 경우 Takehara et al. (2002), Kunida et al. (2009), Okubo and Fujita (2010), Fujita et al. (2015a, 2015b) 등이 헬리콥터와 드론 영상을 이용한 유속 측정을 시도하였다. Tauro et al. (2015)은 드론의 안정적인 호버링에 대한 연구를 수행하였으며, 드론이 일정 시간 동안 1 × 1 m2의 영역 위로 안정적으로 호버링 할 수 있음을 보였다. Detert and Weitbrecht (2015)는 액션캠과 저비용 쿼드콥터로 대규모 유속장을 측정하는 유속계의 적용 가능성을 검토하였다. Detert et al. (2016)은 Murg 강에서 드론 영상을 이용하여 하천의 유량을 산정하는 연구를 수행하였다. 측정한 순간 표면유속장과 난류 지표에 의한 수심 추정치를 도출하였으며 산정한 유량은 ADCP와 비교하였을 때 10% 이내의 오차를 보여 드론 영상을 이용한 하천 유량 측정이 가능함을 보였다. 국내 연구의 경우 Yu and Hwang (2017)은 드론에 비디오카메라와 야간 영상 획득을 위한 원적외선 카메라를 장착하여 한국건설기술연구원 안동하천실험센터에서 표면유속 측정 실험을 수행하였다.
이와 같이 드론 영상을 활용하여 표면유속을 측정하는 연구가 다양하게 진행 중이다. 기존 연구에서 영상을 보정하기 위해 사용되고 있는 방법은 2차원 투영 좌표 변환법으로 (Fujita et al. 1998), 최소 4개의 참조점을 이용하여 영상 왜곡을 보정하는 기법을 사용한다. 그러나 유속 측정 영역이 달라질 경우 참조점을 수표면과 동일한 평면에 다시 설치하고 측량을 수행하여야 한다는 번거로움이 있다. 또한 화각이 좁은 카메라를 사용하는 경우 참조점이 영상 밖으로 벗어나지 않게 하기 위하여 일정 비행 고도 이상을 확보하여야 하는데 이때 영상 분석에 어려움이 있을 정도로 영상의 공간해상도를 확보하지 못할 가능성도 있다. 따라서 이러한 문제를 해결하기 위해 참조점에 의존하지 않고 별도의 참조점 측량 없이 표면유속을 측정할 수 있는 기술에 대한 연구가 필요한 실정이다.
이에 본 연구에서는 드론 영상을 이용하여 하천 유속 측정을 할 수 있도록 렌즈의 초점거리, 픽셀 크기 및 드론의 비행 고도만으로 영상의 화소 당 물리거리를 계산하여 참조점 없이 표면유속을 산정하는 기법을 개발하였다. 또한 표면유속 산정의 정확도를 향상시키기 위해 연속된 영상의 흔들림 보정을 수행하였다. 또한 본 연구에서 개발한 무참조점 기반 표면유속 산정 기법의 검증을 위해 안동 하천실험센터의 실제 흐름에 대해 표면유속을 산정하고 이를 참조점을 이용하는 표면유속 산정 기법으로 구한 표면유속과 비교하였다.
2. 무참조점 표면유속 산정 기법 개발
하천의 표면유속은 단위시간동안 수표면을 흘러간 추적자의 변위로 계산할 수 있다. 마찬가지로 표면영상유속계를 이용한 표면유속 측정 시에는 두 영상 사이의 시간 간격과 두 영상 내 어떠한 추적자의 변위를 통해 유속을 산정한다. 여기서 두 영상 사이의 시간 간격은 동영상으로 촬영되었을 경우 촬영된 동영상의 초당 프레임 수로, 연속 촬영의 경우 초당 촬영 매수로 알 수 있으며 두 영상 내 어떠한 추적자의 변위는 각 영상에서 추적자의 영상 좌표의 차이를 이용하여 계산할 수 있다. 이때 영상에서의 추적자의 변위는 영상 좌표의 단위로 계산된 화소이다. 따라서 해당 영상의 화소 당 실제 물리거리를 안다면 영상 좌표의 단위로 계산된 화소를 실제 물리 변위로 바꿀 수 있고, 영상 내의 추적자의 실제 변위 및 속도를 계산할 수 있다.
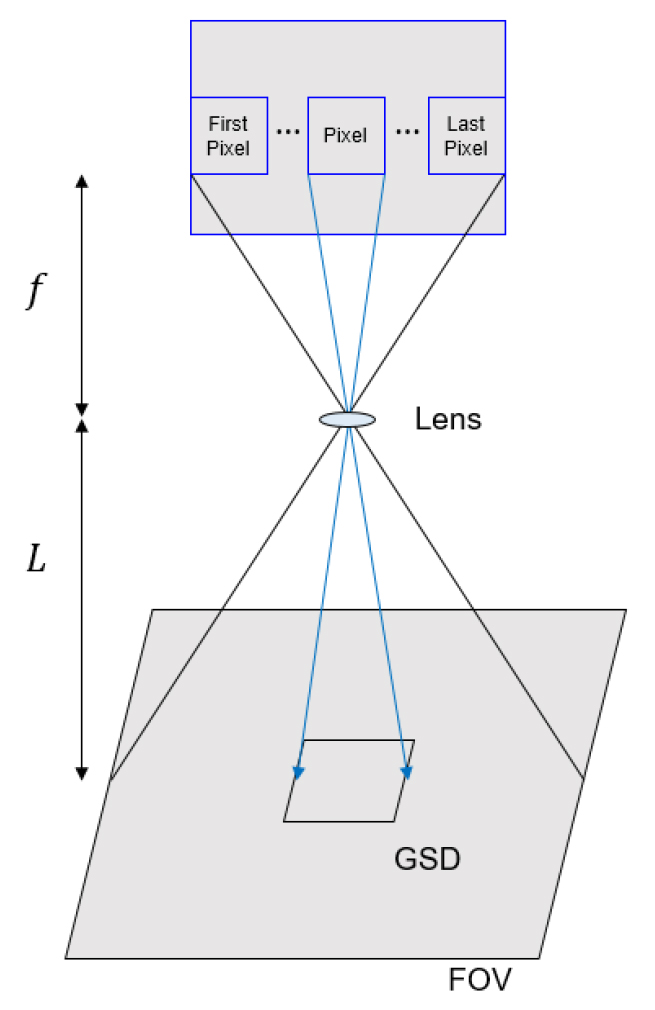
본 연구에서는 화소 당 물리거리 (Ground Sample Distance, GSD)를 계산하기 위해 렌즈의 초점거리 (), 한 화소의 크기 (pixel size) 및 피사체와 렌즈 사이의 거리 ()의 상호 관계를 이용하였다. 여기서 한 화소의 크기는 카메라의 이미지 센서 크기를 영상의 화소 수로 나눈 것이다. Fig. 1은 위의 관계를 간략히 도시한 것이다. 이들 관계를 비례식으로 표시하면 Eq. 1과 같다. 따라서 식 Eq. 2와 같은 관계식을 유도할 수 있다.
예를 들어 렌즈의 초점거리가 3.6 mm, 카메라의 이미지 센서 크기가 6.4 mm × 4.8 mm, 영상의 화소가 1920 × 1080 pixel, 렌즈와 물체 사이의 거리가 50 cm라고 하자. 한 화소의 크기는 이미지 센서 크기를 화소 수로 나눈 0.00333 mm이고 비례식에 의해 GSD는 0.463 mm/pixel (0.00333 mm/pixel × 500 mm/3.6 mm = 0.463 mm/pixel)이 된다. 계산된 GSD는 영상의 각 화소의 모양이 정방형일 경우 종 ‧ 횡 어느 방향에서든 유효하다. 따라서 영상에서 어떠한 물체의 길이는 영상에서 물체가 차지하는 화소 수에 GSD를 곱하여 구할 수 있다. 드론의 경우 기본적으로 지면과 연직한 방향을 바라보고 촬영하기 때문에 드론 영상은 영상 내 모든 화소의 화소 당 물리거리가 같다. 따라서 본 연구에서 개발한 무참조점 표면유속 산정 기법은 드론 영상을 활용한 표면유속 산정에 적합하다고 판단된다.
3. 드론 영상을 활용한 무참조점 표면유속 산정
본 장에서는 2장에서 개발한 무참조점 표면유속 산정 기법의 검증을 적용하고 검증을 수행하였다. 본 연구에서 개발한 기법을 이용하여 표면유속을 산정하기 위해서는 먼저 화소 당 물리거리를 정확하게 산정하는지에 대한 검증이 필요하다. 이에 본 연구에서 개발한 기법으로 영상 내 참조점 사이의 물리거리를 산정하고 측량한 참조점 사이의 거리와 비교하는 방법으로 기법의 검증을 수행하였다. 다음으로 실규모 하천의 실험을 할 수 있는 안동의 하천실험센터에서 표면유속을 산정하고 검증하였다. 표면유속 산정 기법의 검증은 수표면에 설치한 참조점을 이용하여 표면유속을 산정하는 기존 표면영상유속계와 비교하였으며, 접촉식 초음파유속계인 FlowTracker로 측정한 유속과도 비교하였다. 표면유속과 평균유속 사이의 수심평균유속환산계수는 0.85를 사용하였다. 참조점 유무에 따른 유속 값을 비교하였다.
3.1 연구 장비
본 연구에서 드론은 DJI사의 Mavic 2 Pro 제품을 사용하였다 (Table 1). Mavic 2 Pro 제품은 가격이 저렴하고 가벼우며 운용이 쉬워 간단한 교육 후 쉽게 사용이 가능한데다가 기본적으로 GPS, 무선 송수신 장치, 호버링 기능을 자동으로 작동해주고 있다. 드론의 호버링 정확도는 수직으로 ±0.5 m, 수평으로 ±1.5 m 정도이며 1개 장착 가능한 배터리로 최대 29분 비행할 수 있다. 드론에 장착되어 있는 카메라는 최대 4000 × 3000 화소로 사진 촬영이 가능하며 동영상은 3840 × 2160 화소로 초당 30프레임으로 촬영이 가능하다. 연사 촬영 모드도 지원하며 최대 초당 5프레임의 사진을 촬영할 수 있다. 또한 자동 초점 기능과 수동 초점 기능이 있어 필요에 따라 초점을 조정할 수 있으며 카메라의 거치대에는 짐벌이 달려있어 흔들림에 대해 안정적인 영상 취득이 가능하다. 또한 조종기로 카메라의 촬영 각도와 배율에 대한 조작이 가능하고 드론으로 촬영한 영상에 대해 영상 촬영 당시의 시각, GPS 좌표, 고도, ISO, 조리개 값, 3축에 대한 촬영 각도 등의 정보가 메타데이터에 기록된다.
Table 1.
Specification of DJI Mavic 2 Pro
3.2 대상지 선정 및 참조점 측량
본 절에서는 드론을 이용하여 영상 내에 참조점이 담기도록 촬영하고 영상 분석을 통해 참조점 사이의 물리거리를 산정한 뒤 측량한 참조점 사이의 거리와 비교하였다. 또한 고도를 20 m, 30 m, 40 m, 50 m로 달리하여 영상을 촬영하여 고도에 의한 영향이 있는지 분석하였다. 하지만 바람에 의해 드론의 비행고도가 컨트롤러에서 조종한 고도와 상이하여 메타데이터에 기록된 정보를 통해 비행고도를 계산하였으며 실제 비행고도는 각각 20 m, 30 m, 39 m, 49 m로 나타났다. 참조점은 실험수로의 제방을 따라 내려가 수표면에 맞춰 붉게 도색한 테트라포트 모형을 설치하여 사용하였으며 총 4개를 이용하였다 (Fig. 2). 그 후 RTK GPS를 이용하여 측량을 수행하였으며 흐름 방향을 x방향으로 하여 측량 결과를 정리한 결과는 Table 2와 같다. 또한 화소 당 물리거리 산정을 위해 필요한 카메라의 제원과 비행고도에 따른 화소 당 물리거리는 Table 3에 정리하였다.
Table 2.
Physical coordinate of reference points
| Physical coordinate (m) | ||
|
Reference points | 1 | (-0.061, 4.869) |
| 2 | (0, 0) | |
| 3 | (17.353, 0) | |
| 4 | (17.425,4.492) | |
Table 3.
Specification of camera and GSD of each drone height
| Specification of camera | Height (m) | GSD (mm/pixel) |
|
∙ Sensor size 13.2 × 8.8 mm2 ∙ Video resolution 3840 × 2160 pixel ∙ Focal length 10.267 mm | 20 | 6.70 |
| 30 | 10.04 | |
| 39 | 13.06 | |
| 49 | 16.41 |
드론 영상은 기본적으로 지면과 연직한 방향을 바라보고 촬영하기 때문에 영상 내 모든 화소의 화소 당 물리거리가 같다. 따라서 2번 참조점과 3번 참조점 사이의 물리거리만을 비교하여 기법의 검증을 수행하였다. 측량한 결과로 계산하였을 때, 2번 참조점과 3번 참조점 사이의 거리는 17.353 m로 산정되었다. 다음으로 고도별 영상 내의 2번 참조점과 3번 참조점 사이의 영상 좌표와 이를 통해 계산한 영상 좌표의 차이, 화소 당 물리거리를 곱해서 계산된 참조점 사이의 물리거리를 Table 4에 정리하였다.
Table 4.
Difference between calculated distance and measured distance
물리거리 산정 및 검증 결과 측량한 참조점 사이의 거리와 최대 3.47%의 차이를 보였으며 평균적으로 2.67%의 차이를 보임을 확인하였다. 이와 같이 산정한 물리거리가 실측치와 차이나는 것은 비행고도와 독립적인 요인으로 판단된다. 다시 말해, 비행고도가 높거나 낮으면 정확도가 감소하는 경향은 보이지 않는다. 차이를 보인 많은 요인들 중에 가장 크게 작용하는 것은 드론 고도 측정 불확도가 있다고 판단된다. 게다가 오히려 비행고도가 낮을 경우 차이가 크게 날 수 있다. 왜냐하면 고도 물리거리 산정 시 발생하는 상대 불확도는 Eq. 2에 의해 비행고도에 비례하는데, 비행고도 측정 상대 불확도는 비행고도가 높을 때보다 낮을 때 상대적으로 커지기 때문이다. Table 1에 보면 본 연구에 사용한 드론의 비행고도는 ±0.5 m의 수직 정확도를 가지고 있으며 비행고도가 소수점 이하를 표현하지 못하기 때문에 비행고도 측정에 대한 측정 불확도는 ±0.5 m이다. 따라서 이로 인해 물리거리 산정 시 실측치와 차이를 보였다고 할 수 있다.
따라서 드론의 실제 비행고도는 측정된 값에서 최대 1.0 m까지 차이가 날 수 있다. 이를 고려하였을 때 드론의 비행고도별 계산한 참조점 사이의 거리와 측정한 참조점 사이의 거리의 차이는 Table 5와 같다. 드론의 비행고도가 가지는 불확도를 고려하였을 때 계산한 거리와 측정한 거리의 차이는 0 - 7.95%를 보인다. 물론 드론의 비행고도를 정확히 측정하는 것이 계산한 거리와 측정한 거리의 차이를 줄인다고 할 수는 없다. 다만 그 차이에 가장 크게 작용하는 것이 드론의 비행고도 측정 불확도이므로 조금 더 정밀한 장비를 이용하여 드론의 비행고도를 측정할 수 있다면 본 연구에서 개발한 기법의 정확도를 크게 개선할 수 있다고 판단된다.
Table 5.
Difference between calculated distance and measured distance for each drone height
|
Drone height (m) |
Difference (%) |
Real drone height range (m) |
Difference range (%) |
| 20 | 2.81 | 19 - 21 | 0 - 7.95 |
| 30 | 1.97 | 29 - 31 | 0 - 5.37 |
| 39 | 3.47 | 38 - 40 | 0.82 - 6.12 |
| 49 | 2.43 | 48 - 50 | 0.34 - 4.52 |
3.3 표면유속 측정 실험
본 연구에서는 안동 하천실험센터의 실규모 하천 수로에서 개발한 표면유속 산정 기법의 검증을 수행하였다. 안동 하천실험센터에서의 실험은 동일한 유속에서 드론의 비행고도에 관계없이 본 연구에서 개발한 기법을 이용하면 일정하게 표면유속 산정이 가능한지를 검토하고자 하였다. 이에 드론의 비행고도를 20 m, 30 m, 40 m 및 50 m로 달리하여 수표면을 촬영하였으며 Fig. 3과 같다. 하지만 바람에 의해 드론의 비행고도가 컨트롤러에서 조종한 고도와 상이하여 메타데이터에 기록된 정보를 통해 계산하였으며 실제 비행고도는 각각 20 m, 30 m, 39 m 및 49 m로 나타났다. 또한 실험수로에 추적자를 일정 시간 살포하여 높은 고도에서도 수표면의 움직임을 쉽게 가시화할 수 있도록 하였다. 이때 표면유속의 비교를 위해서는 실험수로를 흐르는 유량의 변화가 없어야 한다. 따라서 시간에 따른 유량 변화를 확인하기 위해 하류의 교량에 초음파수위계를 설치하여 실험을 진행하는 동안 시간에 따른 수위를 측정하였다. 실험을 진행하는 동안 초음파수위계로 측정한 수위는 1 cm 내외의 변화를 보였으며 이는 초음파수위계 측정 영역의 일렁이는 수면 파문에 의한 측정값의 불확도로 판단된다. 따라서 실험을 진행하는 동안 시간에 따른 유량 및 표면유속의 변화는 없이 정류조건에서 실험을 실시하였다고 할 수 있다.
본 연구에서 개발한 표면유속 산정 기법의 정량적 검증을 위해 동일한 영상을 이용하되 참조점을 이용하여 측정한 표면유속과의 비교를 수행하고자 하였다. 참조점은 물리거리 산정 및 검증에 사용한 참조점을 사용하였으며 참조점은 흔들림 보정을 위한 특징점으로도 사용하였다.
본 연구에서 개발한 표면유속 산정 기법의 핵심은 별도의 참조점 없이 카메라의 제원과 드론의 비행고도만으로 영상의 화소 당 물리거리를 산정하는데 있다. 본 연구에서 사용한 Mavic 2 Pro 제품의 비행고도에 따른 화소 당 물리거리는 Table 3에 정리되어 있다. 별도의 참조점 없이 상호상관법을 이용하여 계산한 입자군의 속도를 계산하면 단위가 화소인 입자군의 속도가 계산되는데, 여기에 화소 당 물리거리를 곱하면 입자군의 실제 속도를 계산할 수 있다.
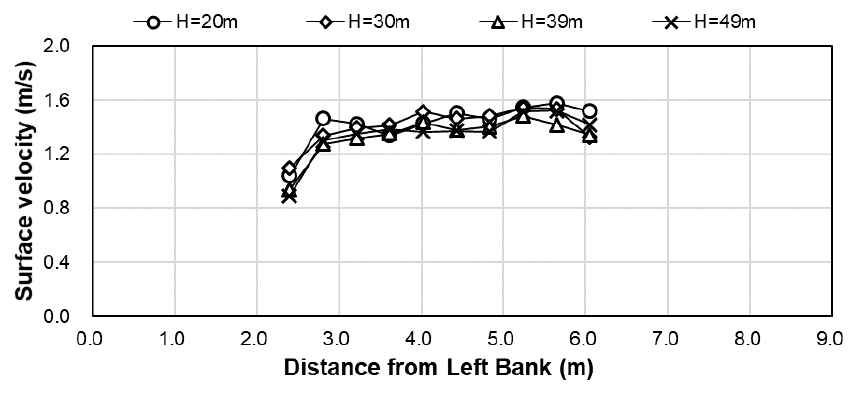
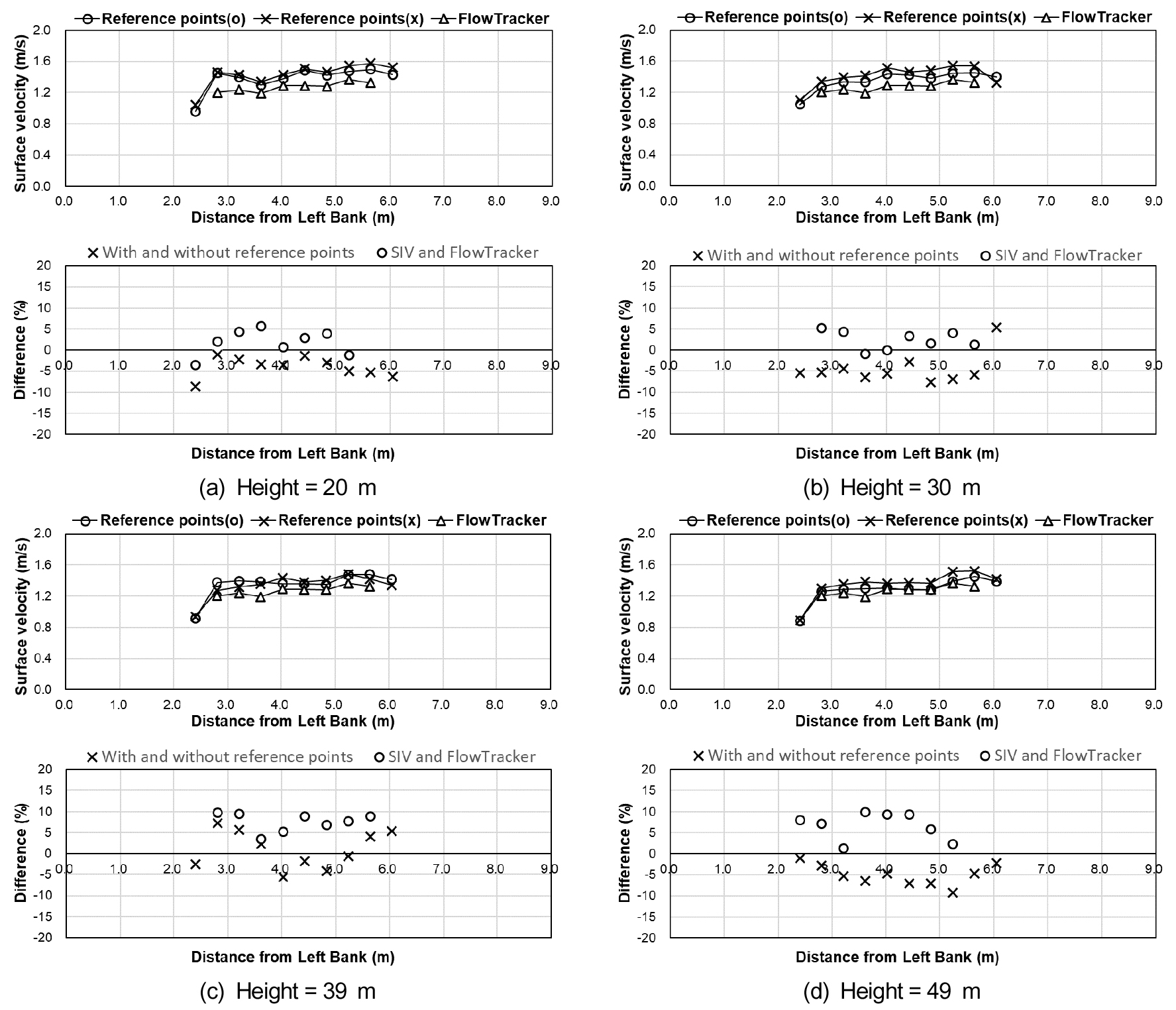
보정을 수행한 영상에 대해 기존 표면영상유속계 프로그램을 이용하여 유속을 산정하였다. 드론의 비행고도에 따라 참조점 없이 표면유속을 산정한 유속은 Fig. 4와 같다. 또한 수표면에 설치한 참조점을 이용하여 산정한 유속과 참조점 없이 산정한 유속을 비교하였다. Fig. 5 (a), Fig. 5 (b), Fig. 5 (c), Fig. 5 (d)는 각각 비행고도 20 m, 30 m, 39 m, 49 m에서 촬영한 영상으로 산정한 유속과 FlowTracker를 이용하여 산정한 유속을 비교한 그래프이며 그 값은 Table 6, Table 7, Table 8, Table 9에 정리하였다. 참조점을 이용하여 산정한 유속과 참조점 없이 산정한 유속의 유속 분포는 일정한 비율로 약간의 차이가 있었지만, 측정한 단면 이후 만곡부로 향하여 우안 쪽의 유속이 빠르게 산정되는 유황을 공통적으로 확인할 수 있었다. 유속 비교 결과 비행고도 49 m에서 최대 9.20%의 차이를 보이지만 평균적으로는 약 4.70%의 차이를 보이는 것을 확인하였다.
Table 6.
Velocity comparison and difference (Height = 20 m)
Table 7.
Velocity comparison and difference (Height = 30 m)
Table 8.
Velocity comparison and difference (Height = 39 m)
Table 9.
Velocity comparison and difference (Height = 49 m)
표면영상유속계 프로그램을 사용하여 산정한 유속과 FlowTracker를 이용하여 측정한 유속과도 비교하였다. 표면영상유속계로 산정한 유속은 표면유속이며 FlowTracker를 이용하여 측정한 유속은 평균유속이기 때문에 둘의 비교를 위해서는 수심평균유속환산계수를 곱해주어야 한다. 일반적으로 수심평균환산계수는 0.84 - 0.87 사이의 값을 사용하며 (Rantz 1982) 본 연구에서는 0.85를 사용하였다. 유속 비교 결과 비행고도 49 m에서 최대 9.90%의 차이를 보이지만 평균적으로는 4.60%의 차이를 보이는 것을 확인하였다.
이렇게 일부 차이가 발생한 원인으로는 표면영상유속계 프로그램의 격자 배치 과정의 한계로, 완벽하게 같은 위치에서 유속을 산정하지 못한 데 원인이 있다고 보인다. 또한 비행고도가 높을수록 화소 당 물리거리가 커져 표면영상유속계의 불확도가 커지는 데에도 원인이 있다. 따라서 이와 같은 유속 산정 불확도를 줄이기 위해서는 향후 표면영상유속계의 불확도 요인에 대한 연구가 필요하다. 다만 유속 분포가 일정한 비율로 차이가 발생하는 이유는 드론 비행고도 측정 해상도에 따른 불확도가 영향을 미친 것으로 보인다. 드론의 비행고도는 영상에 저장된 메타데이터를 통해 계산하였는데, 메타데이터에 저장된 비행고도는 소수점 이하는 표현하지 못한다. 이때 제공되는 비행고도는 자연수로 표현되므로 비행고도 측정에 대한 측정 해상도 불확도가 0.5 m이다. 따라서 비행고도가 실제보다 최대 0.5 m 높게 측정되어 화소 당 물리거리가 크게 산정되었고 결과적으로 참조점 없이 산정한 유속이 더 크게 산정된 것으로 보인다. 향후 드론의 비행고도를 보다 정밀하게 측정할 수 있는 장비를 사용한다면 이에 대한 불확도가 현저하게 줄어들어 보다 정확한 결과를 도출해 낼 수 있을 것이다.
4. 결 론
본 연구에서는 드론 영상을 이용한 표면유속 산정 시 참조점을 이용하는 기존 표면영상유속계를 개선하여 드론의 비행고도와 카메라 제원만으로 참조점 없이 표면유속을 산정하는 기법을 개발하였다. 또한 본 연구에서 개발한 기법의 검증을 위해 안동 하천실험센터의 실규모 하천수로에서 표면유속 산정 실험을 실시하였으며, 그 결과는 다음과 같다.
1) 기존에 드론 영상을 이용한 표면유속 산정 시 영상 변환 및 화소 당 물리거리 산정을 위해 참조점을 이용하는데, 이 때문에 드론의 비행고도와 촬영 영역에 한계를 가지게 되며 이를 개선한 새로운 기법이 필요하다.
2) 본 연구에서 개발한 개선된 표면유속 산정 기법은 드론의 비행고도와 카메라의 제원을 이용한 비례식으로 간단하게 영상 내 모든 영역의 화소 당 물리거리 산정이 가능하며 기존 표면영상유속계와 달리 드론의 비행 고도와 촬영 영역, 분석 영역에 구애받지 않아 드론 영상을 이용한 하천 유속 측정의 강점인 공간적 자유성을 확보할 수 있다는 장점이 있다.
3) 개선된 화소 당 물리거리 산정 기법의 검증을 위해 안동 하천실험센터에서 실험을 실시하였다. 드론의 비행고도를 달리하고 본 연구에서 개발한 기법을 적용하여 참조점 사이의 거리를 산정하였으며 측량한 참조점 사이의 거리와 비교를 수행하였다. 비교 결과 평균적으로 2.67%의 차이를 보여 매우 높은 정확도를 보임을 확인하였다.
4) 개선된 표면유속 산정 기법의 검증을 위해 안동 하천실험센터에서 실험을 실시하였다. 드론의 비행고도를 달리하고 본 연구에서 개발한 기법을 적용하여 표면유속을 산정하였으며 기존의 참조점을 이용하는 유속 측정 방법으로 산정한 표면유속, Flow Tracker로 측정한 유속과 비교를 수행하였다. 표면유속 산정 결과 3가지 유속 측정 방법 모두 흐름 특성에 맞는 유속 분포 및 유황을 공통적으로 확인할 수 있었으며 본 연구에서 개발한 유속 측정 기법을 기존 참조점을 이용하는 유속 측정 방법과 비교하였을 때 유속은 평균적으로 4.70%의 차이를 보이는 것을 확인하였다. FlowTracker로 측정한 유속과 비교하였을 때에도 평균적으로 4.60%의 차이를 보이는 것을 확인하였다.
5) 유속 산정 결과 일부 차이가 나는 이유는 격자 배치 과정에서 발생하는 표면영상유속계 프로그램의 한계와 표면영상유속계의 불확도에 의한 한계도 있지만 드론 비행고도 측정에 대한 측정 해상도 불확도가 크게 작용한 것으로 판단된다. 드론의 비행정보가 저장되는 메타데이터에는 드론의 비행고도가 자연수로 표현되어 측정 해상도 불확도가 0.5 m이며 드론의 비행고도 측정 수직 정확도는 ±0.5 m이다. 이는 화소 당 물리거리 산정 시 크게 영향을 주는 요인이라고 판단된다. 향후 드론의 비행고도를 정밀하게 측정할 수 있는 장비를 사용한다면 이에 대한 불확도가 현저하게 줄어들고 보다 정확하게 표면유속을 측정할 수 있을 것으로 판단된다.
본 연구에서는 기존 드론 영상을 이용한 표면유속 측정 시 발생하는 한계를 극복하고자 참조점 없이 영상의 화소 당 물리거리를 산정하는 무참조점 표면유속 산정 기법을 개발하였다. 안동의 하천실험센터에서 실제로 유속 측정한 결과 기존 표면영상유속계로 측정한 유속과 상당히 비슷한 유속을 측정할 수 있었다. 즉, 본 연구에서 개발한 기법을 이용하면, 참조점 없이 효과적으로 표면유속을 측정할 수 있음을 확인하였다. 다만, 본 연구에서 개발한 기법은 드론의 비행고도 및 카메라의 제원을 이용하기 때문에 비행고도 및 카메라의 제원의 불확도에서 비롯된 유속 측정 불확도가 존재하며 이에 대한 추가적인 연구가 필요한 것으로 판단된다. 향후 본 연구에서 개발한 기법을 이용하면 비행고도와 촬영 영역, 분석 영역에 구애받지 않고 드론을 이용하여 정확도 높은 하천 표면유속을 측정할 수 있을 것으로 기대한다.