1. 서 론

최근 국내에서는 기후변화로 인한 이상기후로 국지성 집중호우가 빈번히 발생하고 있으며 이로 인한 인명 및 재산피해가 지속적으로 발생하고 있다. 집중호우 시 하천의 흐름을 따라 나뭇가지, 토사, 자갈, 유목 등 유송잡물들이 이동하는데 이들이 교각 사이 혹은 암거 등에 퇴적되는 경우 통수능력을 저하시키고 이로 인해 주변지역의 범람가능성을 증가시킨다. 또한 주변의 흐름을 가속시켜 세굴심 증가를 유발하여 수공구조물의 안정성에 영향을 미친다. 올해 집중호우와 태풍으로 국내에서는 소하천에 교량붕괴 사고가 잇따라 발생하였으며 그 원인은 유목들이 교각에 충격을 주어 하중을 증가시키고 교각 주변에 집적되어 유수의 흐름을 가속화하여 세굴을 심화 시켰기 때문이다(Fig. 1). 특히 2000년대 이전에 건설된 교량의 경우 2000년대 이후 건설된 교량에 비해 교각의 경간장이 좁기 때문에 유송잡물이 집적될 가능성이 높아지고 있어 이에 대한 예측 및 대책 마련이 시급하다.

Fig. 1

Bridge collapse and deposition of driftwood around bridge piers (https://news.kbs.co.kr/news/view.do?ncd=5001887).

하천에 설치된 교각 주변에 집적된 유송잡물에 대한 연구를 살펴보면 유목을 대상으로 대부분 연구가 수행되었고 처음 Laursen and Toch (1956)는 모래로 구성된 하상에 설치된 교각 주변에 유목이 집적되는 경우 세굴에 대한 실험을 수행하였다. Melville and Dongol (1992)은 모래로 구성된 하상에 설치된 교각에 유목들이 집적되는 경우 세굴실험을 수행하였고 세굴심을 산정하는 유효폭 개념을 제안하였다. Lyn et al. (2003)은 실내실험수로에서 단일교각을 수로 중앙에 위치시켜 유목의 집적 특성을 검토하였다. 수심이 낮고 유속이 느린 조건에서 실험이 수행되어 결과가 다소 제한적이다. Bocchiola et al. (2006)은 실내수리실험을 통해 유목이 교각 혹은 식생을 통과하는 경우 유목의 거동 특성에 대하여 조사하였다. 유목을 단순화하기 위해 뿌리가 없고 유연하지 않는다는 가정하에 균일한 원통형 스틱을 사용하였고 다양한 조건에서 810개의 테스트를 수행하였다. 이를 통해 교각의 간격과 식생의 밀도 유목의 길이 그리고 유량과 수심을 결합하여 무차원 식을 제시하였다. 7은 실내수리실험을 수행하여 유목의 집적 형상, 위치, 공극률 등에 의한 교각세굴심의 특성을 분석하였다. 유목이 집적되는 경우 세굴심에 영향을 주는 가장 큰 인자는 유목의 수심방향으로 집적된 깊이로 나타났으며 세굴심 및 세굴영역에 영향을 미쳤다. De Cicco et al. (2020)은 수리실험을 통해 다양한 전면부 교각형상에 따른 유목의 집적 가능성과 유목의 거동 메커니즘을 분석하였다. 높은 프루드수 조건에서 정사각형 교각 주변에 유목이 집적될 가능성이 가장 높게 나타났다. Panici and Almeida (2020)는 수리실험을 통해 유목을 단순화한 원통형 스틱과 자연 나뭇가지를 활용하여 교각 주변에서 유목의 집적을 검토한 결과 나뭇가지가 집적이 더 크게 발생하였으며 교각의 형상에 대한 유목 집적의 영향은 정사각형 교각이 가장 크게 나타났지만 그 영향은 미미하다고 보고하였다. Schalko et al. (2020)은 교각 주변에 유목이 집적될 가능성에 대한 경험식을 제시하기 위하여 흐름조건, 교각형상, 교각의 지름, 유목의 길이, 밀도 등을 다양하게 변화시키며 실험을 수행하였다. 이를 통해 하천설계에 적용할 수 있는 경험식을 제안하였다.

많은 연구들이 교각 주변에서 유목 집적 특성 및 거동에 대한 연구를 수리실험을 통해서 수행해왔다. 최근에는 수치모의 통한 연구가 시도되고 있으며 Ushijima et al. (2009)은 3차원 흐름모형과 유목 거동 모형을 개발하였다. 그러나 개발된 모형은 상당한 계산시간이 소요되는 것으로 나타났다. Ruiz-Villanueva et al. (2014)는 2차원 수심적분 흐름모형에 유목 거동모형을 결합된 수치모형을 제안하였고 수리실험과 비교하였다. 수치모형은 유목 거동 및 집적 특성을 잘 재현하였지만 2차원 수치모형으로 부유된 유목에 대한 거동만 계산이 가능하다는 한계가 있다. Kimura and Kitanozo (2020)는 3차원 흐름모형에 2차원 유목 거동모형을 활용하여 만곡수로에서 교각이 배치되는 경우 유목 집적 특성을 분석하였으며 무차원 계수인 drift Richardson number (DRI)에 따른 유목 특성을 분류하였다. 연구결과 DRI > 10인 경우 유목의 거동이 3차원적으로 발생하기 때문에 3차원 흐름모형과 유목 거동모형이 필요하다고 하였다.

따라서 본 연구의 목적은 교각이 존재하는 개수로에서 유목들이 상류에서 유입되는 경우 다양한 수리조건 및 유목의 특징에 따라 유목 집적 및 거동 특성을 수치모의하는 것이다. 이에 3차원 난류흐름과 3차원 유목 거동을 해석할 수 있는 iRic (International River Interface Cooperative) software에 탑재되어 있는 NaysCUBE를 활용하여 수치모의를 수행하였다. 첫째로 NaysCUBE 내에 있는 유목 거동과 관련이 있는 매개변수가 수치모의 결과에 미치는 영향을 검토하였다. 다음 교각주변에서 유목 집적과 관련된 접근유속, 유목 길이의 비, 유목밀도 변화에 따른 교각 주변에서 유목의 거동 및 집적 특성을 분석하였다.

2. 수치해석 방법

2.1 흐름 지배방정식

이 연구에서 적용하는 NaysCUBE의 흐름 지배방정식은 비정상, 비압축성 레이놀즈-평균 나비어 스톡스 (Reynolds-averaged Navier-Stokes, RANS) 방정식이다. 곡선좌표계 (curvilinear coordinate system)에서 연속방정식과 운동량 방정식은 다음과 같다.

여기서 ξ^α는 곡선좌표계의 성분, Vⁱ는 유체의 유속벡터, g는 3차원 자코비안 (Jacobian), p는 압력, ν는 유체의 동점성계수, ρ는 유체의 밀도, Fⁱ는 중력가속도, vⁱ는 난류유속, e^ij는 ∂Uⁱ/∂xⁱ, vIvJ는 레이놀즈응력 텐서이다.

이 연구에서는 공학적 문제에서 널리 사용되는 표준 k-ε모형에 복잡한 이차류와 와류의 특성을 반영할 수 있도록 제안된 비선형 k-ε모형을 적용하여 해석하였다 (Kimura et al. 2009). 본 모형은 유한체적법 (finite volume method)를 적용하였으며 운동방정식과 난류이송방정식의 이송항에 대해서는 시간과 공간적으로 양해법에 기반 3차정확도를 갖는 TVD-MUSCL (Total variation diminishing-monotonic Upwind Scheme for Conservation Laws)기법을 적용하였다.

2.2 유목 거동 지배방정식

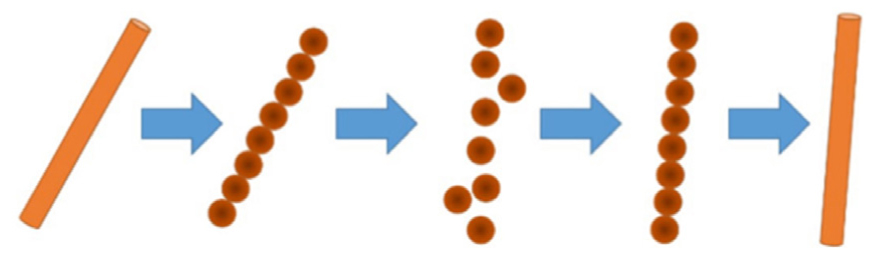
본 모형에서 유목의 운동을 해석하기 위해 Koshizuka (1997)가 개발한 moving particle semi-implicit (MPS) 형태의 입자운동방정식을 적용하였다. 유목의 회전 (rotation) 및 충돌 (collision)에 대한 모델링을 수행하기 위해 유목을 여러 개의 구체 (sphere)로 표현하였다. Fig. 2에 모형에서 계산되는 유목의 운동에 대한 계산과정을 제시하였다. 먼저 계산시간동안 각 구체의 운동을 독립적인 구체의 운동으로 계산하고 무게중심은 각 구체 중심의 좌표값을 평균하여 계산한다. 이후 무게중심 주변의 평균이동속도와 평균각속도를 계산한다. 마지막으로 유목을 구성하는 구체를 다시 유목의 형태인 직선으로 재배열하여 초기의 원통형 스틱형상으로 재구성한다. 각 계산시간마다 이와 같은 과정이 반복하여 계산되며 계산시간간격이 충분히 작다면 원통형 스틱으로 가정한 유목을 여러 개의 구체로 나누어 계산할 수 있다 (Kimura and Kitanozo 2020).

Fig. 2

Computational process for driftwood motion tracking (Kimura and Kitanozo 2020).

유체의 3차원 공간을 따라 움직이는 구체의 운동은 Largangian 입자운동방정식을 이용하여 계산되며 아래와 같다 (Shrestha 2009).

여기서, σ는 유목의 밀도, C_M은 질량계수 (=0.5), C_D는 향력계수 (=1.0), A₂는 2차원 형상계수 (=π/4), A₃는 3차원 형상계수 (=π/6), d는 구체의 지름, u는 유체의 유속벡터, u_p는 구체의 유속벡터, F_p는 구체 상호작용에 의한 반발력, λ_{A_sub}는 구체 투영면적의 침수비, λ_{V_sub}는 구체 체적의 침수비이다. 구체의 상호작용에 의한 반발력은 discrete element method (DEM)으로 계산된다 (Kimura and Kitanozo 2020).

유체 내에서 유목에 의한 흐름 저항을 반영하기 위해 항력을 고려하였다. 유목에 의한 저항은 유목의 형상을 고려하여 모델링되어야 하지만 이는 매우 복잡하기 때문에 유목을 구성하는 각 구체에 의한 항력이 발생하여 흐름에 영향을 주는 것으로 가정하였다. 세부적인 모형에 대한 설명은 iRic (i-ric.org/)의 NaysCUBE 매뉴얼에 기술되어 있다.

2.3 계산 격자 및 경계조건

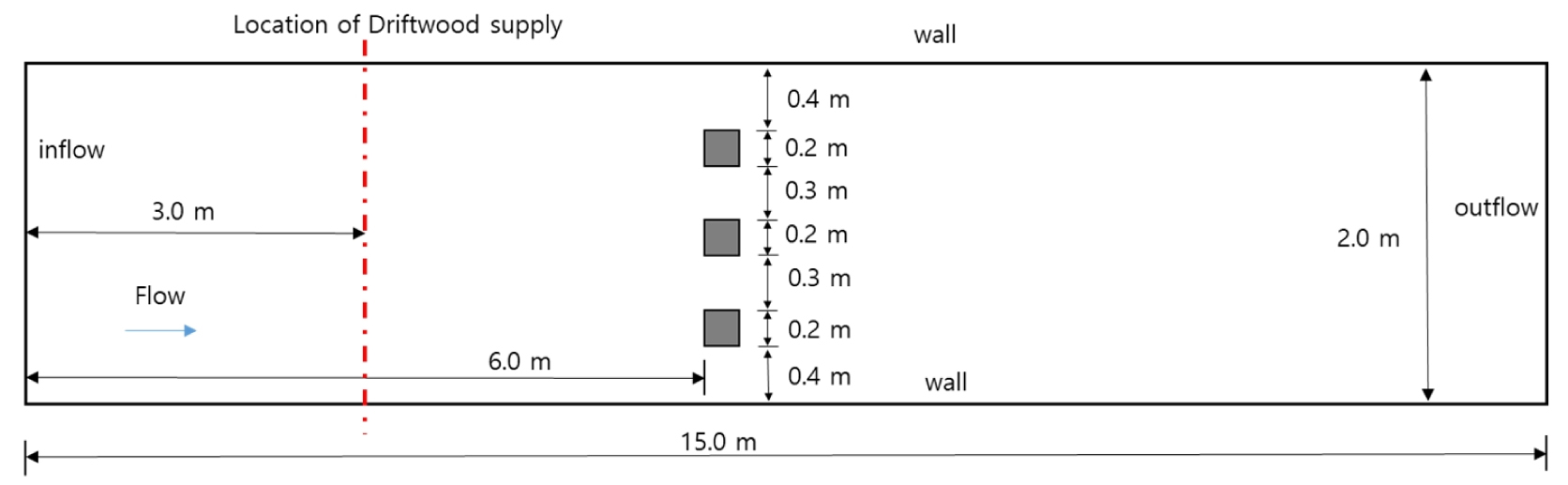
본 연구에서 직선 개수로에 정방형 교각이 존재하는 경우 유목의 집적 특성과 거동을 분석하기 위하여 길이 15.0 m, 폭 2.0 m의 계산영역을 구축하였다 (Fig. 3). 계산격자는 흐름 및 횡 방향으로 0.05 m × 0.05 m의 정방형 격자로 구축하였고 연직방향으로 8개의 격자를 적용하여 총 계산 격자의 수는 96,000개이다. 수로의 경사는 1/1000로 설정하고 상류단에서는 유량 (Q), 하류단에서는 수위 (H) 경계조건은 부여하여 수치모의를 수행하였다. 양측면은 벽 (wall)로 설정하여 모의를 수행하였다. 유량은 0.1 m3/s로 설정하였고 하류 수위를 0.126 - 0.35 m로 변화시켰으며 이는 접근유속 (u₀)이 0.14 - 0.39 m/s, 프루드수 (Fr)는 0.08 - 0.35에 해당하는 조건이다. 유입부로부터 6.0 m 하류에 0.2 m × 0.2 m (w_p) 정방형 교각 3개를 위치시켰으며 교각 사의의 폭 (w_i)은 0.3 - 0.4 m로 설정하였다.

유목 운동에 대한 수치모의는 흐름이 안정화된 이후 교각으로부터 3.0 m 상류 지점에서 초기에 180개의 유목이 공급되는 것으로 설정하였다. 유목은 원통형 스틱으로 설정하였으며 유목의 밀도 (ρ_d)는 이전의 수리실험 및 현장조사 결과를 바탕으로 500 - 900 kg/m3을 고려하였다 (de Cicco et al. 2020, Kimura and Kitanozo 2020, Panici and Almeida 2020).유목의 지름은 0.05 m로 설정하였으며 유목의 길이 (L_d)는 0.4 - 1.2 m를 적용하여 이에 대한 영향을 검토하였다.

Fig. 3

Geometrical configuration and boundary conditions.

3. 수치모의 결과

3.1 유속분포

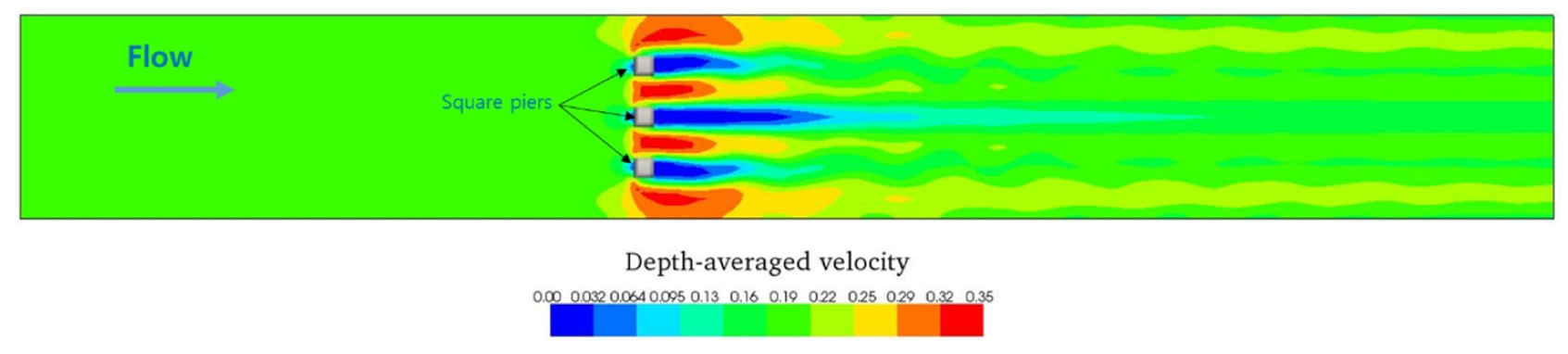
유목운동에 대한 해석을 위해 우선 흐름이 정상상태에 도달할 때까지 수치모의를 수행하였다. Fig. 4는 프루드수가 0.13 (u₀ = 0.2 m/s, h = 0.25 m)인 조건에서 정상상태에서의 수심적분 유속분포를 나타낸다. 상류로부터 균일한 유속이 정방형 교각으로 접근하고 교각 사이를 흐름이 지나가면서 유속이 가속된다. 교각 사이에서 유속은 0.32 - 0.33 m로 접근유속의 2배정도 빠르게 분포하였으며 교각과 교각 사이의 유속이 교각과 벽면 사이의 유속보다 빠르게 나타났다. 교각 하류에서는 교각 후면에서 발생하는 와류 (vortices)가 발생하고 후류영역 (wake region)이 형성되는 것을 볼 수 있다. 후류영역의 길이는 중앙에 위치한 교각 하류에서 상대적으로 길게 형성되는 것으로 나타났다. 이와 같은 흐름특성은 다른 수리조건에서도 유사하게 나타났다.

Fig. 4

Depth-averaged velocity for Fr = 0.13, h = 0.25 m.

3.2 구체 개수에 따른 유목 집적 민감도 분석

이 연구에서 사용되는 유목운동 모형은 단일 개체를 해석하는 것이 아니라 유목을 일정한 크기의 구체로 분할하여 MPS형태의 입자운동방정식을 사용하여 계산한다. 그러므로 구체 개수 및 계산시간 간격에 따라 유목거동에 대한 해석 결과에 영향을 줄 수 있으므로 이에 대한 검토가 필요하다. 이번 연구에서 적용된 계산시간 간격은 △t < 2 × 10^-3s으로 충분히 작다고 판단되어 이에 대한 검토는 수행하지 않고 구체 개수에 따른 민감도만 분석하였다. Fig. 5에는 접근유속0.2 m/s, 수심 0.25 m인 수리조건에서 길이가 L_d = 0.7 m인 유목이 상류에서 유입되는 경우 구체 개수에 따른 수치모의 결과를 비교하였다. 구체의 개수 (N_s)는 3, 5, 7, 10, 15, 20개를 고려하여 t = 40s동안 수치모의를 수행하였다. 구체의 개수에 따라 교각 상류에 유목이 집적되는 특성이 다르게 나타났다. 구체의 개수가 3개로 구성된 유목 거동 및 집적 특성을 보면 교각 주변에 퇴적된 유목의 분포를 명확히 구분하기 어려운 것으로 나타났다. 구체의 개수가 증가할수록 상류에 유목이 퇴적되는 범위가 감소하고 교각 사이로 이동한 유목들의 양이 점점 증가하는 것으로 나타났다. 또한 수치모의 결과를 보면 유목의 구체의 개수가 10개 이상이 되면 유목의 집적 및 이동은 특성은 크게 변화하지 않는 것으로 나타났다.

Fig. 5

Simulated driftwood pattern for different number of spheres.

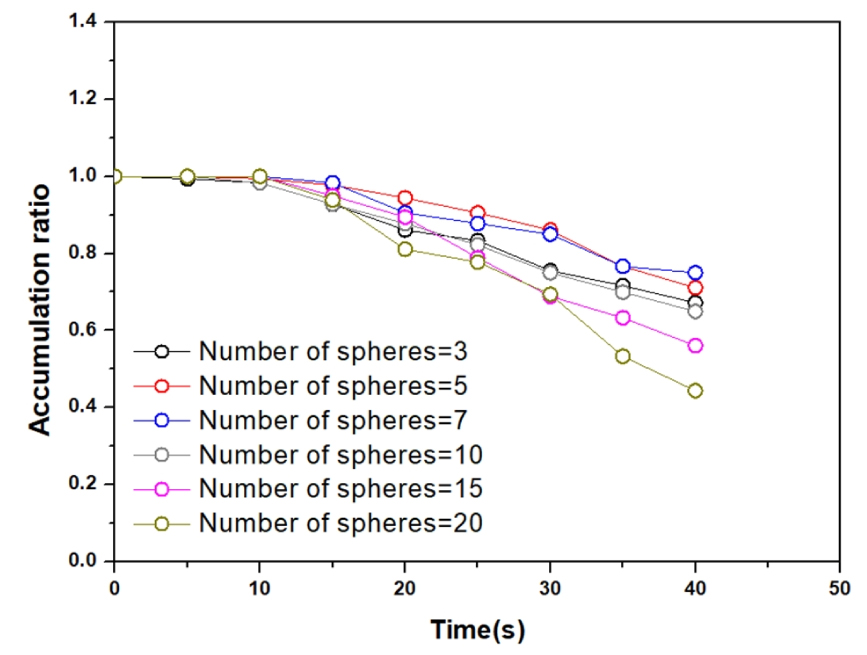
Fig. 6은 시간변화에 따른 유목의 집적비 (accumulation ratio, Ar)를 제시하였다. 여기서 Ar = Q_B/Q_S × 100 (%)로 Q_S는 공급된 총 유목의 수이며 Q_B는 교각에 집적된 유목의 수이다. 시간이 증가하면서 유목의 집적비는 감소하는 경향을 보였다. 유목이 구체의 개수가 N_s = 20인 경우 t = 20s에서 20%가 교각을 통과하여 하류로 이동하였고 t = 30s에서는 30%, t = 40s에서는 급격히 증가하여 55%가 이동하였고 45%가 교각 상류에 집적되는 것으로 나타났다. 수치모의 결과 t = 40s에서 구체의 개수 N_s = 3, 5, 7, 10, 15, 20에 따라 Ar = 67%, 71%, 75%, 64%, 56%, 45%가 교각 상류에 집적되는 것으로 나타났다.

Fig. 6

Accumulation ratio according to the number of spheres.

구체 개수에 따른 유목의 운동 및 집적 특성을 검토한 결과 이 연구에서 N_s ≥ 10을 적용하여 수치모의를 수행하는 것이 적절하다고 판단된다. 구체의 개수가 N_s < 10인 경우 유목을 구성하고 있는 구체 사이의 간격이 커지면서 유목 운동 및 상호작용에 의해 발생하는 오류가 커지는 것으로 나타났으며 이로 인해 적은 개수의 구체로 유목을 재현하는데 한계를 보였다. 구체의 개수가 증가할수록 유목 거동 현상이 정교하게 모의되지만 N_s = 10보다 N_s ≥ 15을 적용하는 경우 계산시간이 5배이상 소요되는 것으로 나타났다. 그러므로 계산시간 및 모의결과를 바탕으로 이후 다양한 조건에서 수치모의 시 구체의 개수는 N_s = 10을 사용하여 계산을 수행하였다.

3.3 접근유속에 따른 유목 집적 특성

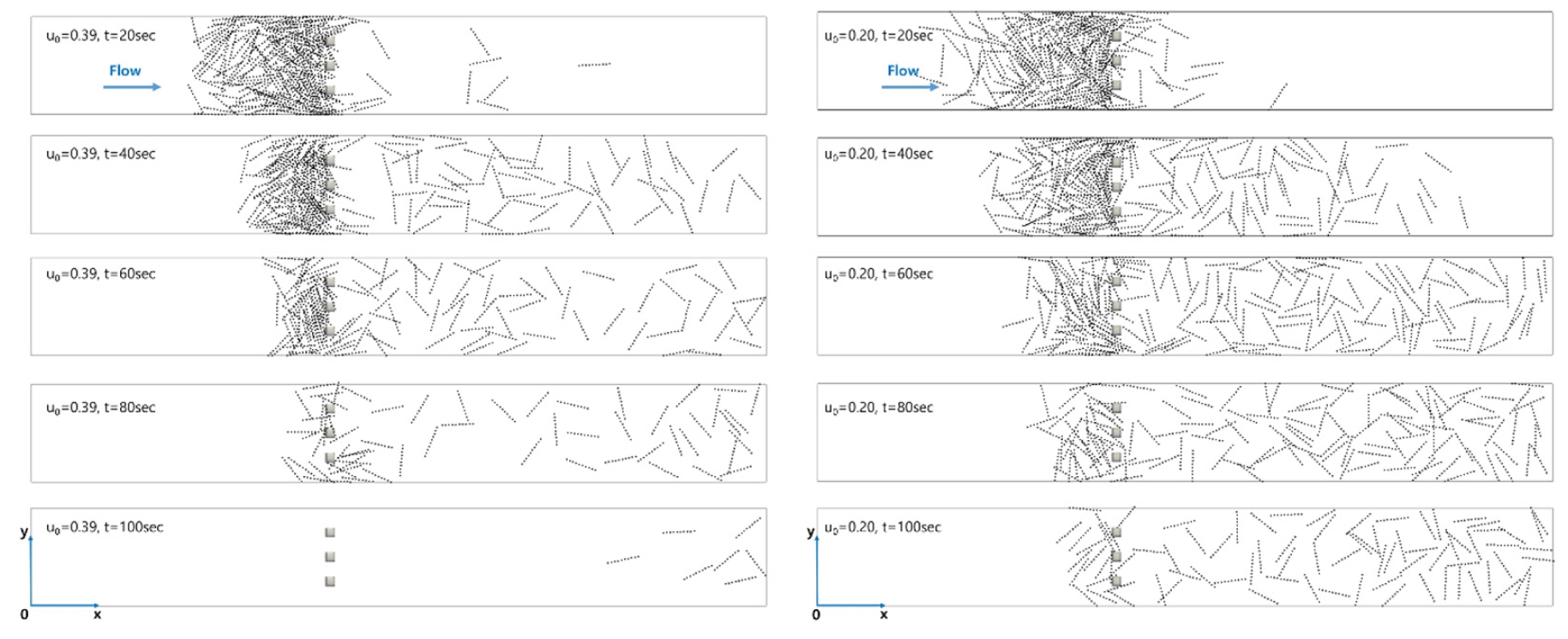
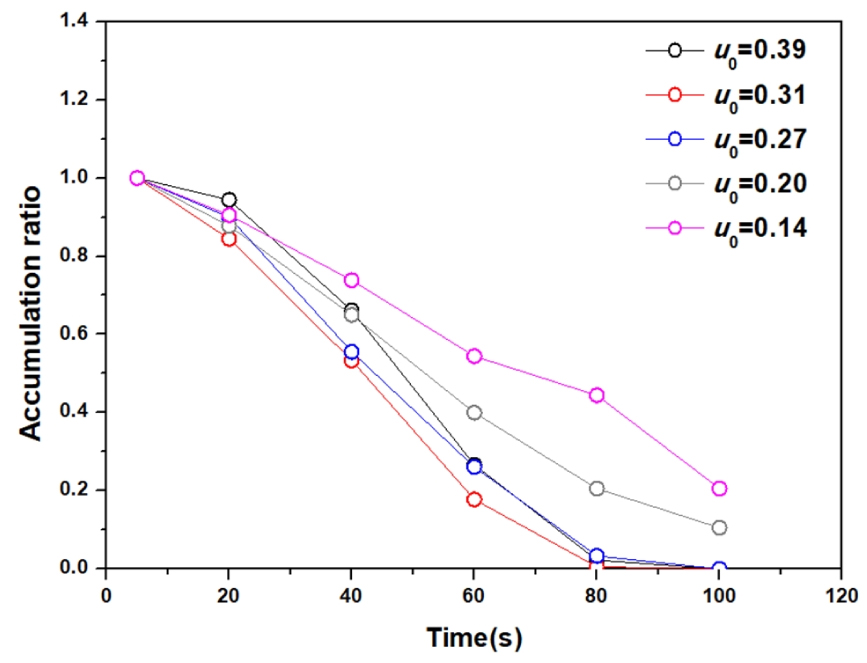
접근유속에 따른 유목이 교각에 집적되는 비 (Ar)와 거동 특성을 검토하였다. 수치모의에 적용된 유목의 길이는 L_d = 0.7 m이며 u₀ = 0.14 - 0.39 m/s에 해당된다. Fig. 7에 접근유속 u₀ = 0.39 m/s와 0.2 m/s에 대한 시간에 따른 유목 이동 및 집적의 특성을 도시하였다. 접근유속 u₀ = 0.39 m/s인 경우 t = 20s에는 대부분의 유목 집적되는 현상을 보이고 상대적으로 폭이 넓은 교각과 벽면 사이로 일부 유목이 하류로 이동하였다. 시간이 지나면서 교각 주변에 집적되어 있던 유목들이 교각 사이를 통과하여 하류로 이동하였고 이로 인해 교각 상류에 유목이 퇴적된 범위는 감소하였다. t = 100s에는 상류에서 공급된 모든 유목들이 교각 하류로 이동하는 것으로 나타났다. 접근유속이 감소하면 유속이 교각 주변에 집적 혹은 정체되는 시간이 증가하는 것으로 나타났으며 하류에서도 유목이 이동하는 속도가 감소하는 것으로 나타났다. 이러한 현상은 Schalko et al. (2020)의 실험결과와 일치하였다. Schalko et al. (2020)은 접근유속이 증가하면 집적비가 감소하고 접근유속이 감소하면 유목이 교각에 접근하여 집적될 가능성이 더욱 증가한다고 하였다. 접근유속이 빠른 경우에는 교각 주변의 난류와 상호작용에 의해 발생하는 수면파에 의해 유목들이 교각사이로 이동이 더욱 원활해진다고 하였다.

Fig. 7

Comparison of driftwood motion: u₀ = 0.39 m/s (left) and u₀ = 0.20 m/s (right).

Fig. 8은 시간변화에 따른 유목의 집적비를 나타낸다. 시간이 증가하면서 유목의 집적비는 감소하는 것으로 나타났고 접근유속이 증가할수록 더욱 급격히 감소하는 것을 확인할 수 있다. 접근유속이 u₀ = 0.14 m/s인 경우 t = 40s에 Ar = 74%, t = 60s에 Ar = 54%로 나타났으며 t = 100s에는 21%가 교각 주변에 집적되어 있는 것으로 나타났다. 반면 접근유속이 u₀ = 0.39 m/s로 증가하면 t = 40s에 Ar = 66%, t = 60s에 Ar = 27%로 나타났으며 t = 80s가 지나면서 교각 주변에 집적되어 있던 유목들이 하류로 이동하였다. 접근유속이 교각 주변에 유목이 집적되는 비 (Ar)에 상당히 영향을 미치는 것으로 나타났고 접근유속 증가는 유목의 집적 가능성을 감소시키는 것으로 확인되었다. Schalko et al. (2020)은 유목이 2차원 거동이 지배적인 경우 수심의 영향을 받지 않으며 유속에 의해 유목의 집적 특성이 변화한다고 하였다. 이를 통해, 접근유속이 교각 주변의 유목 집적에 중요한 인자인것으로 판단된다.

Fig. 8

Accumulation ratio versus time for different Froude number.

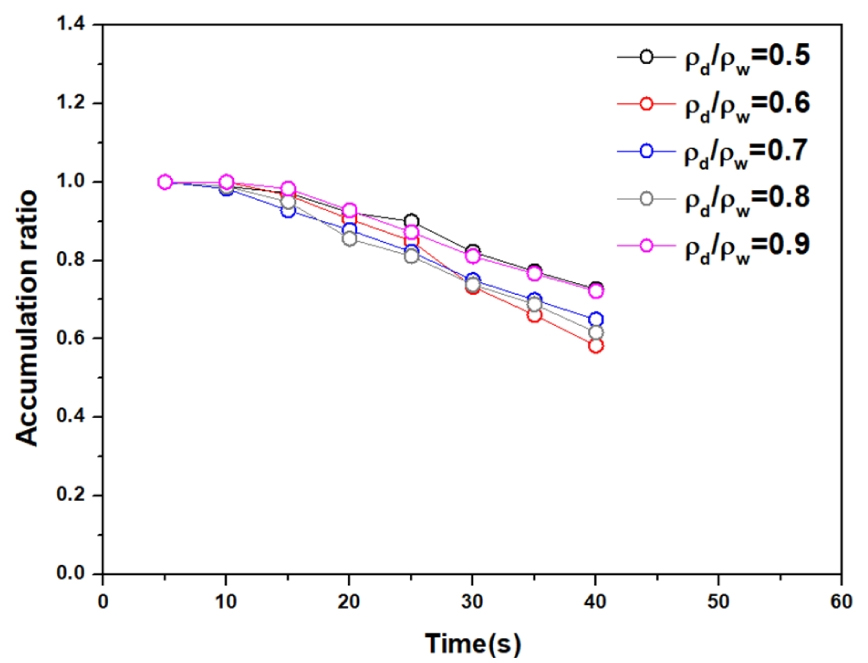
3.4 밀도비에 따른 유목 집적 특성

유목의 밀도는 공간적 계절적 변화에 따라 다르게 나타난다. De cicco et al. (2020) 계절변화에 따라 유목의 밀도 (ρ_d)가 700 - 900 kg/m³를 갖는다고 하였고, Panici and Almeida (2020) 450 - 550 kg/m³를 고려하여 수리실험을 수행하였다. 이에 본 수치모의에서는 500 - 900 kg/m³ (ρ_d/ρ_w = 0.5 - 0.9)의 유목의 밀도를 고려하여 유목 집적 특성을 검토하였다. 밀도비 (ρ_d/ρ_w)에 관계없이 유목의 집적비는 시간에 따라 감소하는 것으로 나타났다. 유목의 집적비는 t = 25s까지 유사하게 나타났지만 t = 30s 이후에는 ρ_d/ρ_w = 0.6, 0.7, 0.8의 경우 집적비가 줄어드는 것으로 나타났다. 그러나 밀도비에 따라 교각 주변에서 유목의 집적비는 평균적으로 ±7% 범위 내에서 변화하는 것으로 나타나 접근유속에 비해 변화의 폭이 작은 것으로 보인다. Schalko et al. (2020) 역시 수리실험을 통하여 밀도비 ρ_d/ρ_w = 0.46, 0.85, 1.32에 따른 집적비를 검토한 결과 평균적으로 ±3.75% 범위 내에서 변화하는 것을 확인하여 밀도에 영향은 무시할만한 인자라고 제시하였다. 이번 수치모의 결과도 밀도비에 영향이 미미한 것으로 나타나 크지 않을 것으로 판단되며 이에 대한 영향을 양호하게 해석하고 있음을 확인할 수 있다.

Fig. 9

Accumulation ratio versus time for different density ratio.

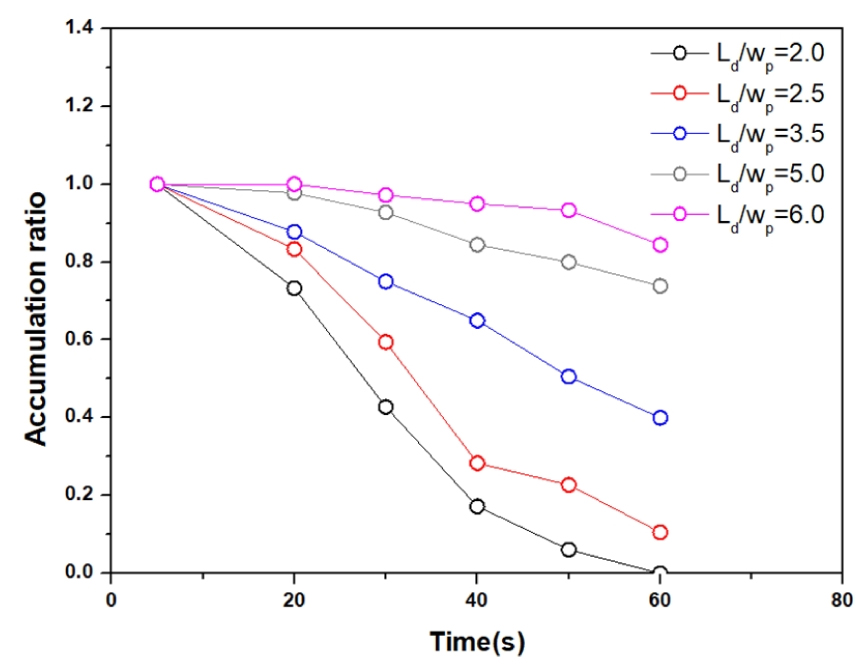
3.5 길이비에 따른 유목 집적 특성

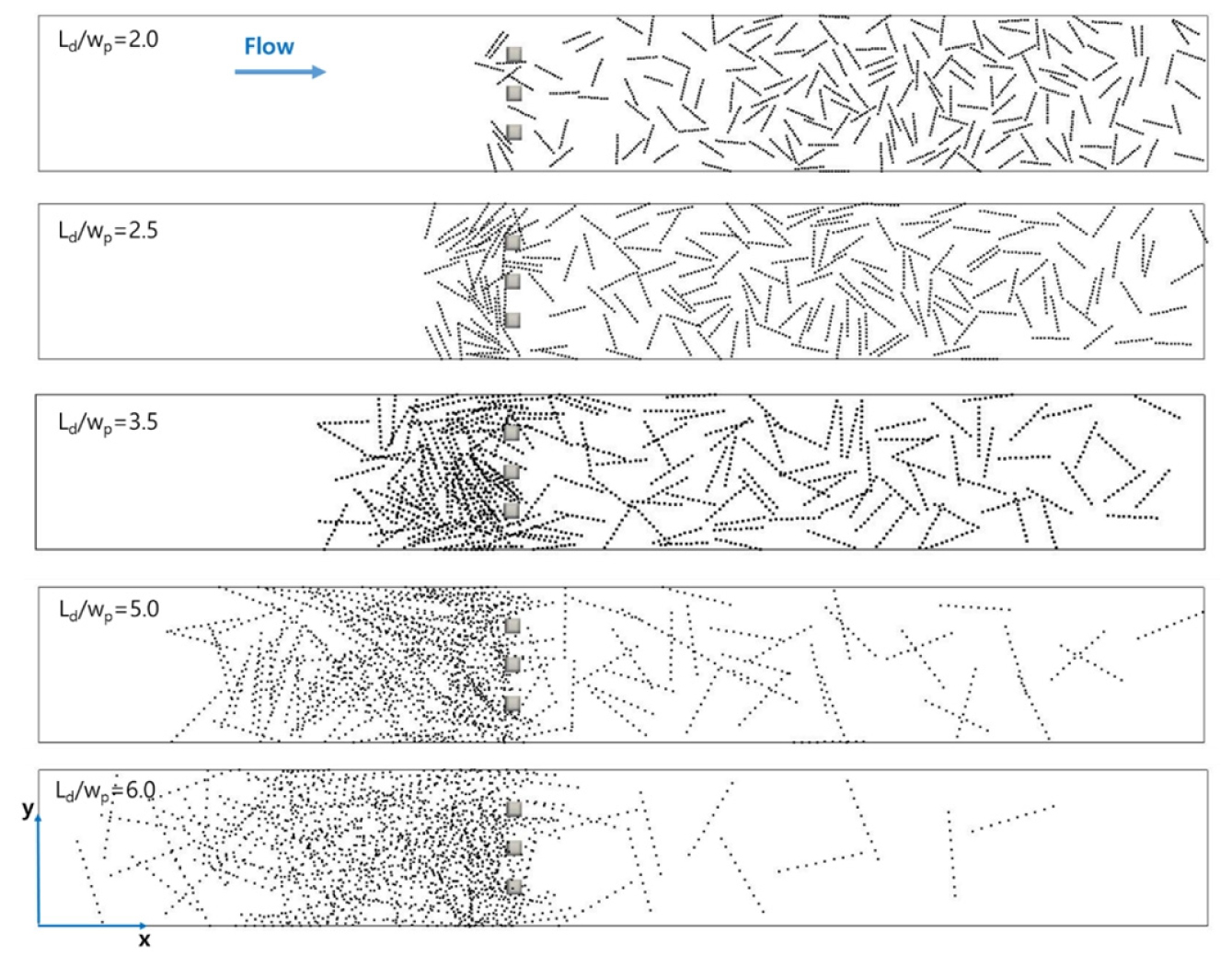
길이비 (L_d/w_p) 변화에 따른 교각 주변의 유목 거동 특성과 집적비를 검토하였다. L_d/w_p = 2.0, 2.5, 3.5, 5.0, 6.0을 고려하였으며 흐름조건은 u₀ = 0.196 m/s, h = 0.25 m/s이다. Fig. 10은 t = 50 s에서 길이비에 따른 유목의 집적 및 거동 패턴을 나타낸다. L_d/w_p = 2.0인 경우 상류에서 유입된 대부분의 유목들이 교각 사이를 통과하여 하류로 이동하는 것으로 나타났다. 길이비 (L_d/w_p)가 증가하면 교각 주변에 집적되는 유목의 비가 증가하는 것으로 나타났으며 퇴적된 영역의 범위가 점점 상류로 증가하는 것으로 나타났다. 특히 L_d/w_p ≥ 5.0인 경우 교각 상류에 집적된 유목들이 교각 하류로 서로 상호작용하면서 이동하지 못하고 집적되어 정체되는 현상이 발생하였으며 교각으로부터 4.2 m (L_d/w_p = 5.0), 4.9 m (L_d/w_p = 6.0)까지 확장되는 것으로 나타났다.

Fig. 10

Simulated driftwood deposition patterns for different length ratio at t=50sec.

Fig. 11에는 유목 길이비에 따른 집적비 변화를 나타내었다. L_d/w_p = 2.0인 조건에서는 t = 10s 이후 유목의 집적비가 급격하게 감소하는 것을 볼 수 있다. t = 20s에서 27%, t = 40s에서 83% 교각 하류로 이동하였고 t = 60s에서 상류에서 유입된 모든 유목들이 하류로 이동하였다. L_d/w_p = 3.5인 조건에서는 t = 20s에서 12%, t = 40s에서 35%가 교각 하류로 이동하였고 t = 60s에는 40%가 상류에 집적되는 것으로 나타났다. L_d/w_p = 2.0의 조건과 비교했을 때 집적비가 2배 이상 증가하였다. L_d/w_p = 6.0인 조건에서는 상류에서 공급된 유목이 대부분 하류로 이동하지 못하고 집적되는 것으로 나타났으며 시간이 경과하여도 집적비 감소는 미미하였다. 집적비는 t = 40s에서 5%, t = 60s에서 15%로 나타났다. 길이비는 교각 주변의 유목 집적비와 특성에 상당히 영향을 미치는 것으로 나타났으며 주요한 인자인것으로 판단된다. 이러한 결과는 기존의 수리실험 결과와 일치하는 것으로 나타났다. Schalko et al. (2020)은 동일한 수리조건에서 유목의 길이가 L_d = 0.1, 0.2, 0.4 m일 때 집적비는 21%, 40%, 58%로 증가한다고 하였다. 특히 길이비는 유목의 밀도비 및 접근유속보다 더욱 민감한 인자인것으로 나타났다.

Fig. 11

Accumulation ratio versus time for different length ratio.

4. 결 론

본 연구에서는 3차원 난류 흐름과 유목 거동을 해석할 수 있는 수치해석모형을 활용하여 교각주변에서 유목의 집적 및 거동 특성을 수치모의하였다. 유목의 3차원 운동은 MPS형태의 입자운동방정식을 적용하여 해석하였으며 수치모의를 통해 얻은 결론은 다음과 같다.

1) 유목을 단일 개체로 해석하지 않고 MPS형태의 입자기반모형을 사용하여 이에 대한 검토를 수행하였고 구체의 개수에 따라 유목 거동의 특성 및 집적비가 변화하는 것으로 나타났으며 계산시간 및 수치모의 결과를 고려하여 본 연구에서는 N_s = 10을 사용하는 것이 최적인것으로 나타났다.

2) 유목의 집적비는 접근유속 (u₀)과 길이비 (L_d/w_p)에 따라 증가하는 것으로 나타났으며 특히 길이비가 집적비 및 유목의 거동 특성에 영향을 미치는 주요한 인자임을 확인하였다.

3) 유목의 밀도는 유목의 집적비 및 거동 특성에 대한 영향이 미미한 것을 나타났다.

3차원 흐름과 MPS형태 기반의 유목 거동 모형을 활용하여 교각 주변의 유목 집적 및 운동 해석에 대한 적용성은 본 수치모의를 통해 확인되었다. 그러나 적용성을 확대하기 위해서는 MPS형태 기반의 유목 거동 모형에서 구체의 개수 및 크기와 흐름에서 해석되는 격자와의 관계를 명확히 제시할 필요가 있다. 향후 유목 집적에 따른 상하류 수위 및 유속변화에 대한 연구도 지속적으로 수행 되어야할 것이다.