1. 서 론
2. 카메라 캘리브레이션
2.1 렌즈 왜곡의 종류 및 렌즈 왜곡의 수학적 모델
2.2 실험에 사용한 장비의 카메라 캘리브레이션 결과
3. 영상 내 위치에 따른 변위 산정 결과 비교
4. 결 론
1. 서 론
표면영상유속측정법은 영상을 이용한 비접촉식 유속 측정 방법으로 카메라 외에 별도로 고가의 장비를 구매할 필요가 없어 경제적일 뿐 아니라 기존 유속측정 방법에 비해 안전하다는 장점을 갖고 있는 하천 유속 측정 방법이다. 표면영상유속측정법은 수표면을 촬영한 연속된 두 영상에서 입자군의 명암값 분포를 상호상관법을 이용하여 계산하여 입자군의 변위를 계산하고 이를 두 영상 사이의 시간 간격으로 나누어 입자군의 이동 속도를 산정하는 방법이다 (Fujita et al. 1998). 표면영상유속측정법은 타 유속 측정 장비에 비해 장비 구성과 측정 방식이 매우 간단하기 때문에 경제적이고 신속한 유속 측정이 가능하며 비접촉식 유속 측정 방법이므로 안전하며 흐름 영역의 유속장을 동시에 측정할 수 있어 급변하는 유속 변화를 정확히 측정할 수 있다는 장점이 있다 (Kim et al. 2011). 표면영상유속측정법은 1990대 중반에 일본에서 처음으로 개발되어 하천 유속 측정에 적용되었다 (Fujita and Komura 1994, Aya et al. 1995, Fujita et al. 1997). Fujita and Komura (1994)와 Aya et al. (1995)은 비스듬한 각도로 촬영한 비디오 영상을 분석하기 위한 기법을 개발하였고, 이를 이용하여 하천 제방에서 획득한 영상을 이용하여 유속장을 계산하였으며, 이를 시작으로 Meselhe et al. (2004), Roh (2005), Hauet et al. (2008), Dramais et al. (2011), Fujita and Kunita (2011), Kantoush et al. (2011), Kim et al. (2011) 및 Muste et al. (2011)에 의해 하천 또는 실험실의 수리 계측에 다양하게 활용되었다.
표면영상유속측정법으로 산정한 유속의 정확도를 높이기 위해서는 영상 내 두 입자군의 변위를 정확하게 계산하여야 한다. 하지만 표면영상유속측정법을 이용하여 변위를 계산할 경우 다양한 요인에 의해 실제 변위와 차이가 나며 이는 표면영상유속측정법으로 산정한 유속의 불확도 요인이 된다. 현재까지 밝혀진 표면영상유속측정법의 불확도 요인으로는 Kim (2006)이 추적자 투하, 조명 촬영, 이미지 촬영, 이미지 변환, 이미지 처리 및 후처리의 여섯 단계로 나누어 각 단계별로 정의한 총 27가지와 Visualization Society of Japan (2002)는 교정, 자료 수집, 자료 처리 및 계측 원리로 나누어 정의한 총 36가지가 있다. 따라서 열거된 오차 요인들이 유속 산정 결과에 어떻게 영향을 미치는지에 대한 연구와 유속 산정 결과에 영향을 미치는 추가적인 불확도 요인에 대한 연구가 필요하다.
카메라를 이용하여 실제 하천 수표면을 촬영한 영상은 카메라 렌즈에 의한 왜곡이 필연적으로 발생하게 된다. 이는 영상 내 입자군의 변위 산정 결과에도 영향을 미치며 결과적으로 유속 벡터의 산정 결과에도 영향을 미친다. 하지만 표면영상유속측정법을 이용한 기존 연구에서는 변위 산정 시 카메라 왜곡에 의한 영향을 정량적으로 고려하지 않고 있는 실정이다. 따라서 표면영상유속측정법을 이용한 표면유속 측정 시 정확도를 높이기 위해서는 카메라 왜곡에 의한 변위 측정 정확도 평가가 필요하다.
카메라 왜곡에 의한 영향 분석을 위해서는 먼저 영상에 발생하는 왜곡량을 정량적으로 표현할 필요가 있다. 아무리 왜곡이 작은 카메라를 사용하더라도 카메라와 렌즈의 특성에 의해 왜곡은 필연적으로 발생하며 그 왜곡량은 카메라에 따라 다르고, 같은 종류의 카메라라고 할지라도 제조상에서 발생하는 오차에 의해 왜곡량은 다르다. 카메라 측량에 사용되는 전문가용 카메라의 경우 이러한 카메라와 렌즈의 특성을 제공해주지만, 일반 비전문가용 카메라는 카메라와 렌즈의 특성이 제공되지 않거나 제공된 값이 실제 값과 차이가 난다. 따라서 사진측량학에서도 다양한 방법을 이용하여 카메라의 왜곡량을 정량적으로 계산하고 영상에 발생하는 왜곡을 보정하여 사용하고 있다.
따라서 본 연구에서는 실제 하천의 표면유속 측정에 사용하는 디지털카메라와 스마트폰 카메라로 촬영한 영상을 대상으로 변위 산정 시 발생하는 카메라 왜곡의 영향을 분석하였다. 먼저 카메라 왜곡의 영향을 정량적으로 분석하기 위하여 카메라 캘리브레이션을 통한 카메라 내부 파라미터를 계산하여 영상에 발생하는 왜곡량을 이론적으로 산정하였다. 그리고 영상 왜곡이 변위 산정에 미치는 영향을 확인하기 위하여 각각의 카메라로 조밀한 정사각형 격자 형태의 패턴을 촬영하여 왜곡 보정 전후의 영상에서 촬영된 격자의 크기를 비교하는 실험을 수행하여 영상 왜곡에 의한 변위 산정 정확도를 평가하였다.
2. 카메라 캘리브레이션
2.1 렌즈 왜곡의 종류 및 렌즈 왜곡의 수학적 모델
카메라에서 상은 피사체로부터 반사된 빛이 렌즈를 통과하여 이미지 센서에 투영되어 나타난다. 그러나 렌즈의 형상, 수차, 주점 왜곡 등의 영향으로 상이 이미지 센서에 정확하게 맺히지 못하여 왜곡이 발생하게 된다. 이 중 렌즈의 수차에 의해 발생하는 왜곡은 방사 방향의 왜곡과 접선 방향의 왜곡으로 나누어진다.
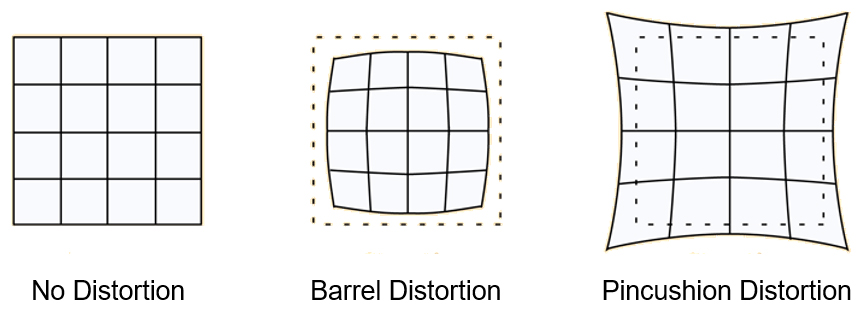
방사왜곡 (radial distortion)은 일반적으로 카메라 영상 가장자리 부근에서 발생하며 렌즈의 종류에 따라 볼록 렌즈에 의해 영상의 모서리가 주점으로 가까워져 측면이 부풀어 오른 형태인 술통형 왜곡 (barrel distortion)과 오목 렌즈에 의해 영상의 모서리가 주점으로부터 멀어져 측면이 오목하게 휘어진 형태인 바늘꽂이형 왜곡 (pincushion distortion)으로 나뉜다 (Fig. 1). 방사왜곡은 렌즈의 굴절률에 의해 발생하는 것으로 렌즈 중심에서 멀어질수록 왜곡이 크게 나타난다. 따라서 영상의 왜곡 정도가 영상 중심에서 멀어질수록 크게 나타난다. 방사왜곡은 Eq. 1과 같은 방사왜곡 보정식으로 보정이 가능하다 (Lee et al. 2016).
여기서 , 은 방사왜곡이 보정된 영상 좌표, , 는 왜곡된 영상 좌표, , , 는 방사왜곡 보정계수, 은 영상 중심으로부터의 거리이다.
접선왜곡 (tangential distortion)은 카메라 제조과정에서 생기는 왜곡으로 렌즈와 이미지 센서와의 평행이 맞지 않거나 복합렌즈를 사용할 때 각 렌즈의 중앙이 맞지 않아 발생하는 왜곡이다. 대부분 카메라 제조과정에서 영상의 이미지 센서를 카메라 안쪽에 붙이는 작업을 할 때 센서와 렌즈가 완벽하게 평행이 이루어지지 않는 경우 왜곡이 발생하며 비선형적인 타원형 형태로 왜곡도가 분포한다. 접선왜곡에 대한 보정식은 Eq. 2와 같다 (Lee et al. 2016).
여기서 , 는 접선왜곡이 보정된 영상 좌표, , 는 왜곡된 영상 좌표, , 는 접선왜곡 보정계수, 은 영상 중심으로부터의 거리이다.
본 연구에서는 카메라 캘리브레이션에 관한 다양한 연구에서 가장 많이 사용되는 수학적 모델 해석 알고리즘인 Zhang (2000)이 제안한 다항식 모델을 사용하였다. Zhang (2000)이 제안한 다항식 모델은 여러 장의 영상을 취득하여 각각의 2차원 영상과 3차원 공간상의 실제 점 사이의 관계를 매칭시켜 왜곡을 발생시키는 카메라 내부 파라미터를 산정하는 방법으로 많은 논문에서 사용된 검증된 방법이고 OpenCV 소스코드가 다양한 언어로 구현되어 있어 접근이 용이하다는 장점이 있다.
2.2 실험에 사용한 장비의 카메라 캘리브레이션 결과
공기 및 지상 사진측량 전용 카메라와 달리 일반 비전문가용 카메라는 카메라와 렌즈의 특성이 제공되지 않거나 제공된 값이 실제 값과 차이가 나는 경우가 많다. 따라서 일반 카메라를 사용할 경우 반드시 카메라 캘리브레이션을 통해 카메라와 렌즈의 왜곡 보정계수 및 내부 파라미터를 구해야 한다. 일반적으로 표면유속 측정에 사용하는 카메라는 왜곡이 적은 표준렌즈가 장착된 카메라를 사용한다. 따라서 본 연구에서는 화각 (Field Of View, FOV)이 75°, 72°인 2대의 카메라를 사용하였다. 연구에 사용한 카메라와 렌즈의 제원은 Tables 1 and 2와 같다.
Table 1.
Specs of the FUJI cameras used in this study
Table 2.
Specs of the iPhone cameras used in this study
카메라 캘리브레이션은 3차원 공간상의 점과 2차원 영상에 맺힌 2차원 좌표를 맵핑하는 것으로 시작한다. 영상 내의 한 점을 실제 3차원 물리좌표의 원점으로 설정하고 영상 내의 좌표를 실세계 3차원 좌표로 매칭시키는 것이다. 다시 말해, Eqs. 1 and 2의 보정식을 이용하여 영상 내의 좌표와 실세계 좌표 사이의 방정식을 해석하기 위해 영상 내 각 점의 영상좌표 (, )을 실세계의 물리좌표 (, )와 매칭시키는 것이다. 캘리브레이션에 사용하는 영상의 매수는 경험적으로 20 - 30개의 이미지를 사용하는 것이 정확도가 높으며 Zhang (2000)은 오차를 줄이기 위해 최소 5개 이상의 이미지를 사용하여야 한다고 하였다. 이 작업은 수동으로 일일이 입력하는 방법을 사용하기도 하지만 일반적으로 Fig. 2와 같이 체스보드와 같은 격자형 패턴을 인쇄하여 여러 각도에서 촬영하는 방법을 사용한다. 촬영에 체스보드나 균일한 간격으로 찍혀있는 원형 패턴을 사용하는 이유는 코너 검출 등의 영상처리 알고리즘을 이용하여 영상 내의 좌표를 쉽고 정확하게 찾을 수 있기 때문이다. 체스보드 패턴을 촬영하여 카메라 캘리브레이션을 수행할 때 주의할 점은 촬영한 패턴이 영상에 상당한 영역을 차지하도록 가까이에서 촬영하고, 왜곡이 크게 발생하는 영상의 패턴이 들어가도록 여러 장을 촬영하여야 한다는 점이다. 카메라 캘리브레이션 결과 본 연구에서 사용한 두 카메라의 내부 파라미터는 Tables 3 and 4와 같고 이를 토대로 그린 두 카메라의 왜곡 분포도는 Figs. 3 and 4와 같다.
Table 3.
Camera calibration results (FUJI)
| Intrinsic parameter | Value |
| 3,092.54 | |
| 3,083.73 | |
| 1,524.51 | |
| 2,034.49 | |
| 0.1819 | |
| -0.6807 | |
| 0.7909 | |
| 0.0031 | |
| 0.0036 |
Table 4.
Camera calibration results (iPhone)
| Intrinsic parameter | Value |
| 3,236.93 | |
| 3,232.35 | |
| 1,919.16 | |
| 1,091.14 | |
| 0.2063 | |
| -0.9110 | |
| 1.2278 | |
| -0.0006 | |
| 0.0016 |
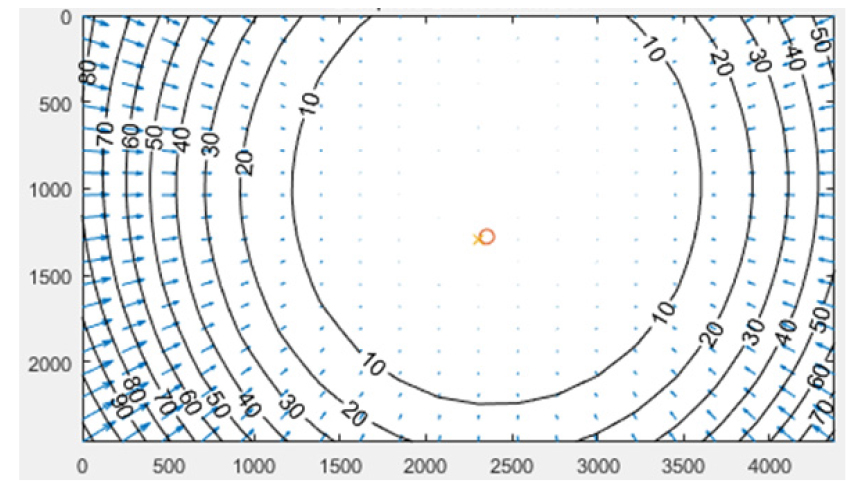
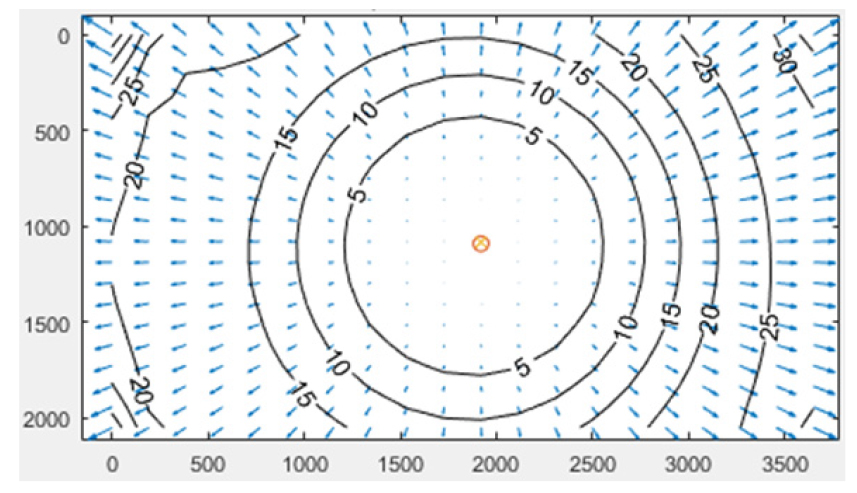
카메라 캘리브레이션 결과를 토대로 그린 왜곡 분포도에서 화살표가 의미하는 것은 왜곡이 없는 영상과 비교하였을 때 영상 내 주점을 중심으로 해당 화소의 왜곡이 발생한 방향이며 왜곡 분포도의 등고선에 쓰인 숫자가 의미하는 것은 왜곡 보정 전과 비교하여 영상 내 주점에서부터의 왜곡 발생 화소 수이다. 다시 말해 화살표가 바깥쪽으로 향하는 것은 카메라 왜곡의 영향으로 영상 내 점의 위치가 실제보다 바깥쪽에 맺힌다는 뜻으로 바늘꽂이형 왜곡을 나타내며, 화살표가 안쪽으로 향하는 것은 영상 내 점의 위치가 실제와 달리 안쪽에 맺힌다는 뜻으로 술통형 왜곡을 나타낸다고 할 수 있으며 숫자가 클수록 왜곡의 크기가 그다는 것을 의미한다. 카메라 캘리브레이션 결과 FUJI 카메라는 전체적으로 술통형 왜곡을 보이며 영상 좌하단에서 최대 약 100화소의 왜곡이 발생하는 것을 확인하였다. 또한 스마트폰 카메라는 전체적으로 바늘꽂이형 왜곡을 보이며 영상 좌상단에서 최대 약 35화소의 왜곡이 발생하는 것을 확인하였다.
3. 영상 내 위치에 따른 변위 산정 결과 비교
앞에서도 언급했듯이, 표면영상유속측정법을 이용한 유속은 연속된 영상에서 상호상관법으로 계산한 입자군의 변위를 시간간격으로 나누어 산정한다. 연속된 영상 사이의 시간간격은 촬영한 동영상의 초당 프레임 수를 이용하면 비교적 정확하게 계산할 수 있으나, 변위 측정에는 여러 가지 요인들에 의한 불확실성이 내포되어 있다. 본 연구에서는 여러 요인 중 카메라 왜곡이 변위 산정 시에 미치는 영향을 분석하였다. 변위 산정 시 카메라 왜곡이 미치는 영향을 분석하기 위해 연구에 사용한 각각의 카메라로 Fig. 5와 같이 간격이 가로, 세로 2 mm로 일정한 정사각형 격자를 촬영하고, 왜곡 보정 전후의 영상에서 격자의 크기를 비교하였다. 촬영한 격자의 크기는 한 칸이 영상 내에서 20화소 정도로, 4K영상을 수표면과 5 m정도 떨어진 제방에서 촬영하였다고 가정할 경우 실제 격자 길이는 약 6 cm 정도이다.
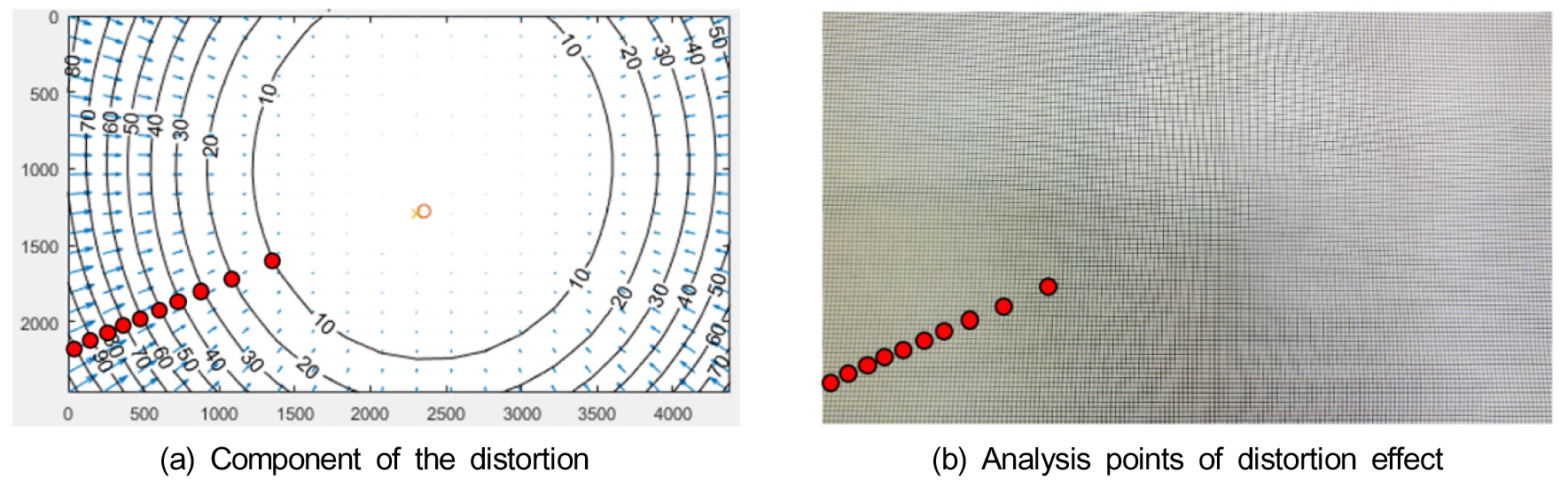
본 연구에서 사용한 카메라로 촬영한 영상의 왜곡량을 정량적으로 알 수 있는 것은 각각의 카메라의 왜곡 분포도에 나타나는 왜곡된 화소 수이다. 왜곡 분포도 (Figs. 3 and 4)를 보면 카메라 왜곡은 영상 내 주점에서 0이며 영상 테두리로 갈수록 크게 나타난다는 것을 알 수 있다. 따라서 영상 내에서 위치에 따라 왜곡 정도가 다르기 때문에 영상 내 위치에 따라 카메라 왜곡이 변위 산정에 미치는 영향도 다르다. 이에 본 연구에서는 변위 산정 시 카메라 왜곡의 영향을 영상 내 위치에 따라 분석하였다. 영상 내 위치에 따른 변위 산정 시 카메라 왜곡의 영향을 보기 위하여 격자의 크기를 영상 내 다양한 위치에서 측정하였고 그 위치는 왜곡 분포도의 각각의 등고선이 그려지는 영역을 기준으로 하여 비교하였다.
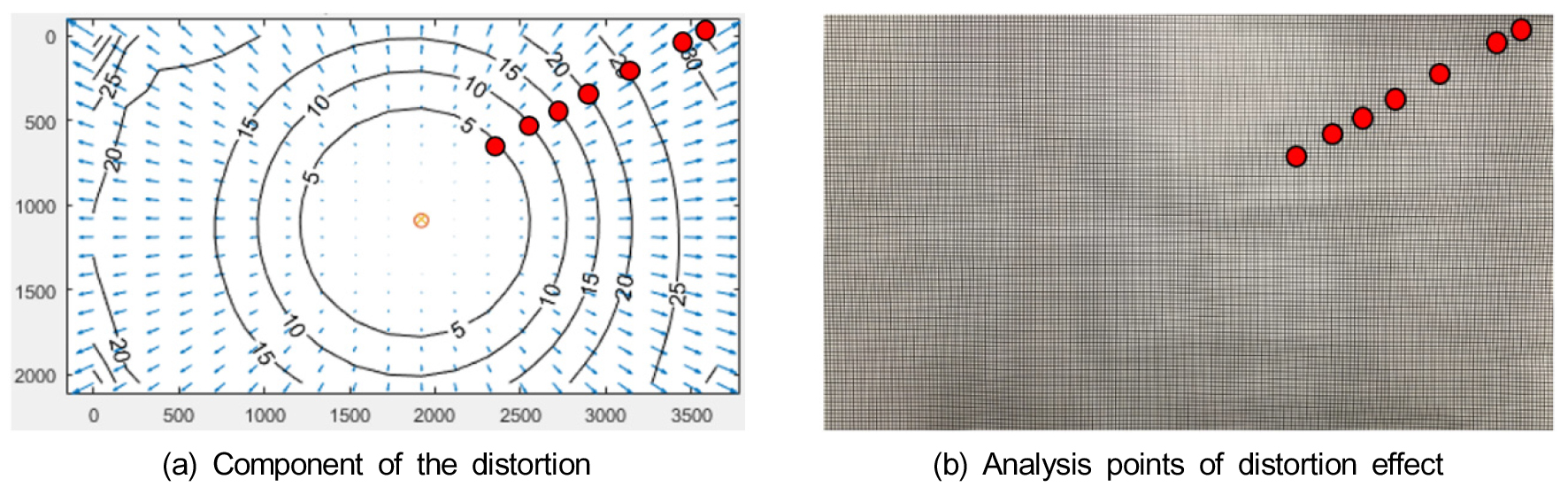
영상 내 위치별 카메라 왜곡의 영향 분석을 위해 Figs. 6 and 7과 같이 왜곡 분포도 내에 왜곡의 크기를 나타내는 각각의 등고선이 그려지는 곳에서 격자 한 칸의 크기를 산정하여 왜곡 보정 전후를 각각 비교하였다. 카메라 왜곡에 의한 변위 산정 영향은 Eqs. 3 and 4에 의해 계산하였으며, 왜곡된 영상에서 산정한 격자의 길이와 왜곡 보정 후의 영상에서 산정한 격자의 길이 차이를 왜곡 보정 후의 영상에서 산정한 격자 길이로 나누어 계산하였다.
Table 5는 FUJI 카메라로 촬영한 영상에 대해 수행한 영상 내 위치에 따른 변위 산정 영향 분석 결과를 나타낸 것으로 영상 주점에서 멀어질수록 왜곡에 의한 변위 산정 영향이 커지는 것을 확인하였다. 영상 테두리에 가까울수록 그 영향이 커져 왜곡이 100화소 발생하는 곳에서는 최대 8.10%의 변위 차이가 발생하였으며 왜곡이 90화소 이하로 발생하는 곳에서는 모두 변위 차이가 5% 미만으로 발생하였다. 이때 분석에 사용한 영상에서 격자 한 칸의 변위가 20화소 정도로, 변위 측정 시 필연적으로 발생하는 1화소의 불확도가 5%의 변위 측정 불확도를 유발한다. 이를 고려하면 변위 차이가 5% 미만으로 발생하는 곳은 카메라 왜곡에 의한 영향이 거의 없다고 판단된다.
Table 5.
Difference of displacement before and after distortion correction (FUJI)
| Distortion amount |
Difference of displacement (pixel) |
Difference of displacement (%) |
| 10 | 1 | 2.46 |
| 20 | 1 | 3.63 |
| 30 | 1 | 3.39 |
| 40 | 1 | 3.58 |
| 50 | 1 | 2.28 |
| 60 | 1 | 2.35 |
| 70 | 1 | 4.34 |
| 80 | 1 | 4.39 |
| 90 | 1 | 4.70 |
| 100 | 2 | 8.10 |
스마트폰 카메라로 촬영한 영상에 대해 수행한 영상 내 위치에 따른 변위 산정 영향 분석 결과는 Table 6과 같다. FUJI 카메라와 마찬가지로 영상 주점에서 멀어질수록 왜곡에 의한 변위 산정 영향이 커지는 것을 확인하였다. 영상 테두리에 가까운 왜곡 정도가 35화소 발생하는 곳에서는 최대 5.63%의 변위 차이가 발생하였다. 하지만 변위 측정 시 발생하는 불확도를 고려하면 카메라 왜곡에 의한 변위 산정 시의 영향이 매우 작게 나타난다고 판단된다.
4. 결 론
본 연구에서는 표면영상유속측정법을 이용한 유속 측정 시 카메라에 의한 영상 왜곡이 미치는 영향을 분석하고자 두 가지 카메라로 격자를 촬영하여 카메라 왜곡 보정 전후 영상에서 각각 변위를 산정하고 비교하여 카메라 왜곡이 변위 산정 시에 미치는 영향과 영향을 미치는 영상 내 범위를 분석하였으며, 그 결과는 다음과 같다.
1) 카메라 렌즈 왜곡은 촬영에 사용한 모든 카메라에 대해 발생하며 이로 인해 발생하는 왜곡은 사용한 카메라에 따라 다르기 때문에 왜곡 보정을 수행하기 위해서는 카메라 캘리브레이션을 통해 왜곡 보정계수와 내부 파라미터를 산정하여야 한다.
2) 카메라 왜곡의 영향은 영상 내 주점에서 0이며 영상 테두리로 갈수록 커지는 비선형적인 형태를 보여 영상 내 위치에 따라 변위 산정 시의 영향이 다르기 때문에 본 연구에서는 영상 내 위치에 따라 각각 변위 산정 영향 분석을 수행하였다. 연구에 사용한 두 카메라 중 FUJI 카메라의 경우 영상 왜곡 보정 전후 영상 테두리 부근에서 최대 8.10%의 변위 차이를 보였다. 영상 중심 부근에서는 5% 미만의 변위 차이를 보였으며 이는 변위 산정시 발생하는 측정불확도를 고려하였을 때 작은 값이라고 판단된다. iphone 카메라의 경우 영상 왜곡 보정 전후 영상 테두리 부근에서 최대 5.63%의 변위 차이를 보였으며 FUJI 카메라와 마찬가지로 영상 중심 부근에서는 5% 미만의 변위 차이를 보이는 것을 확인하였다.
3) 카메라 왜곡에 의한 변위 산정 시의 영향은 영상 테두리로 갈수록 크게 나타나며 영상 중심 부근에서 거의 나타나지 않았다. 본 연구에서 사용한 FUJI 카메라는 일반적인 카메라에 비해 테두리에서 최대 100화소의 영상 왜곡을 발생시킬 만큼 왜곡량이 큰 카메라지만 영상 대부분의 영역에서 5% 미만의 변위 차이를 보였다.
본 연구에서는 표면영상유속측정법을 이용한 표면유속 산정 시 발생하는 다양한 요인들을 배제하고 카메라 왜곡이 변위 산정 시에 미치는 영향을 보고자 정지된 영상을 이용하였다. 향후 카메라 왜곡이 표면영상유속측정법을 이용한 표면유속 산정에 미치는 영향에 대한 면밀한 분석을 위해 실험수로 등 실제 흐름에 대한 카메라 왜곡의 영향 분석이 필요하며, 본 연구 결과들은 카메라 왜곡이 표면영상유속측정법을 이용한 표면유속 산정시 미치는 영향과 카메라 왜곡의 영향을 받지 않는 영상 내 유속 산정 영역 등을 결정하는데 기초자료로 활용될 것으로 기대한다.